5.2 傅里叶变换的理解
5.2.1 Pre Knowledge : Time Domain And Frequency Domain
时域：以时间作为参考来观察动态世界世界的方法，称为时域分析。
频域：如果时域分析是以时间为轴，那么世间万物都是出于改变的状态。如果存在另一种方式来观察世界，并且这个世界是一成不变的话，你会不会觉得我已经疯掉了，这个方式就是频域分析。
频谱图：我们刚刚求的的公式
$$\text{5.1.2} \quad \lim_{T\rightarrow\infty} f_T(t) = \frac {1}{2\pi}\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt \space e^{i\omega t} d\omega \tag{5.1.2}$$
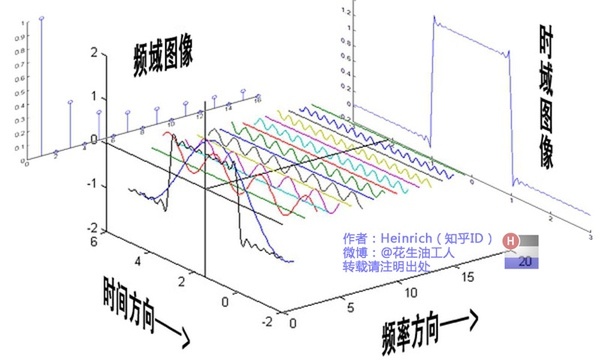
就是一个对于时间频率的三维的频谱图。
-
:trackball: 傅里叶变换：从时域或空域（原始信号）转到频域，它通过分解信号成正弦或余弦波,以频率和幅度来表达信号。 时域 → 频域
-
:trackball: 傅里叶逆变换：从频域转换回到时域或者空域，它可以通过频域表达或者重构出原始信号。 频域 → 时域
我们现在在回来查看傅里叶变换和傅里叶逆变换，所谓频域就是消除时间的影响，而时域就是消除频率的影响。傅里叶变换从时域变成频域，也就是要对上面的重积分对定义域内的时间做积分： $F(\omega) =\int_{t=-\infty}^{t=+\infty}\lim_{T\rightarrow\infty} f_T(t)~dt = \int_{-\infty}^{\infty} f(t)e^{-i\omega t}dt \quad \text{From 5.1.3}$
而傅里叶逆变换，则是对定义域内的频率做积分，傅里叶逆变换是在进行了傅里叶变换之后才能够进行的操作：$\int_{\omega=-\infty}^{\omega=+\infty} \lim_{T\rightarrow{\infty}}{f_T(t)}~d\omega = \frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega t}d\omega \quad \text{From 5.1.4}$
如果上图频谱图从侧面进行观察，我们将得到频域图或者时域图，如果我们往下观察会得到什么呢？相位谱。 为什么要提到相位谱，因为不管是频域图还是时域图，都是存在信息缺失的。不同的相位决定了波的位置，所以对于频域分析，仅仅有频谱是不够的。
5.2.2 相位谱（phase spectrum）
在进行从下面往下看之前先了解如下公式，这个公式叫做基础正弦波公式：
$$
f(t) = A\sin{(\omega{t} + \varphi )} \tag{One Standard Signal}
$$
上述 $A$ 表示振幅，$\omega$ 表示角频率，$\varphi$ 为初相，$t$ 表示时间，$f(t)$ 表示动点的位置。
- 频率(Frequency): $\color{brown} \omega$
- 频率表示信号震荡的快慢。频率越高，信号的变换越快；频率越低，信号的变化就越慢。 在傅里叶变换中我们可以得到信号在不同频率 $\omega$ 上的频域表达 $F(\omega)$ ，这些频率的成分就构成了原始信号。通过频率，我们判断信号中哪些速率的频率占据主导。在图形中，低频表示图像平滑变化，高频表示图像细节与边缘。频率的单位是 赫兹$\text{(Hz)}$ 。
- **简而言之：**频率表示信号的快慢，决定信号中的代表什么样的变化特征。
- 幅度(Amplitude)：$\color{brown} A$
- 幅度表示信号成分大小或强度。在傅里叶变换中成分$F(\omega)$的大小就是幅度。幅度决定了该频率成分在重构原信号中的贡献程度。幅度较大表示该频率在信号中占有较大权重。幅度的单位是 毫米$\text{(mm)}$。
- **简而言之：**幅度表示信号强度,决定该频率成分的重要性。
- 相位(Phase)：$\color{brown} \omega{t}+\varphi$
- 相位表示信号的位置或状态,以度数或弧度为单位测量。它决定了信号成分的正弦或余弦形式。相位不同会导致信号的位置、振幅及波形都发生改变。单位是弧度制 $\text{rad}$ 。
单位的转换：$①1\text{Hz} = 1\text{s}^{-1}\Rightarrow frequency=\frac{1}{T} = \frac{1}{s} = 2\pi{f} \quad ②\omega = \frac{2\pi}{T} = 2\pi{f} \Rightarrow \text{rad/s}$
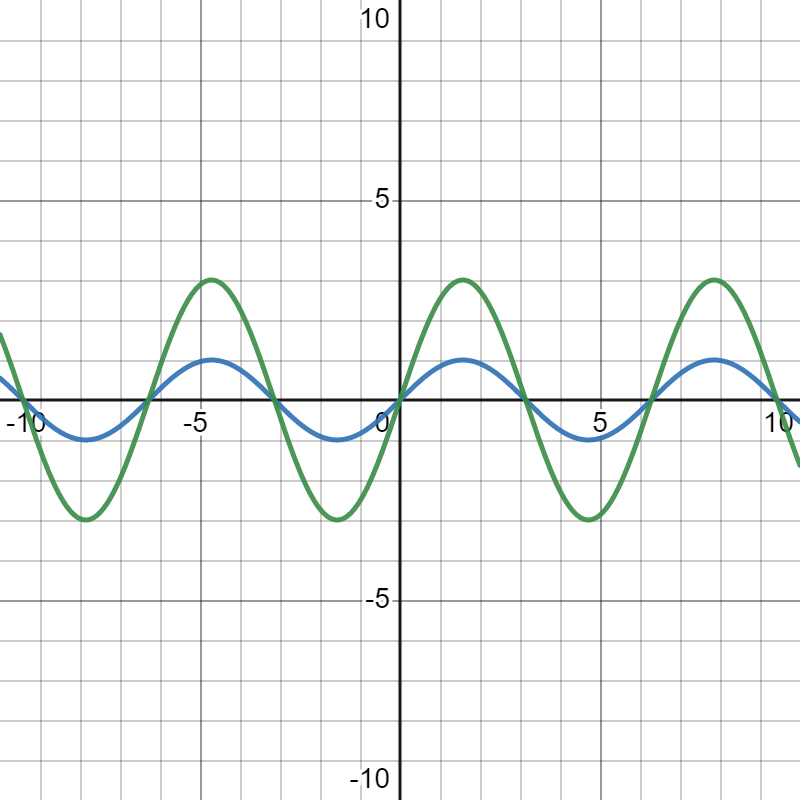
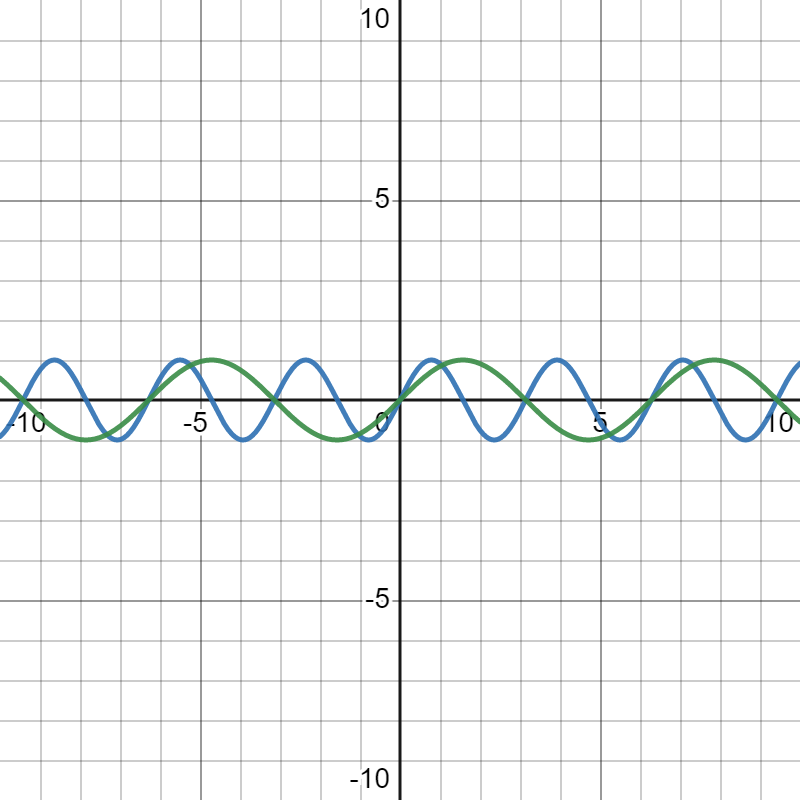
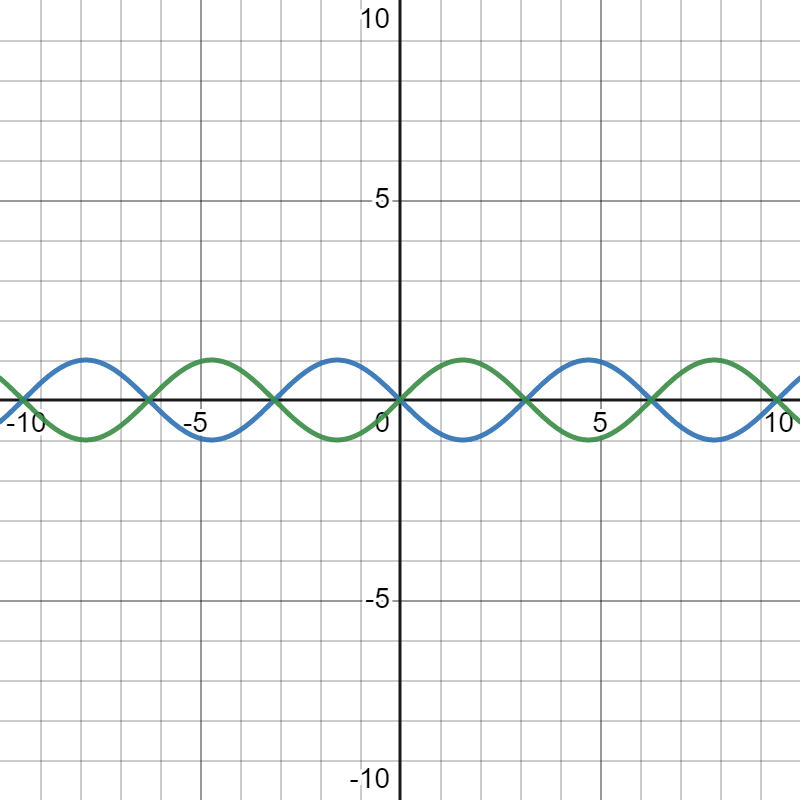
上面的$\text{1,2,3}$ 引用了GPT的回答，简单来说就是，幅度控制了振幅强度（左一 ：$\color{blue}\sin{x},\color{green}3\sin{x}$ 区别），频率控制了波的形状（中间：$\color{blue}\sin{x},\color{green}\sin{2x}$）,而相位控制了图像的位移（右一：$\color{blue}\sin{(x+\pi)},\color{green}\sin{(x)}$）
-----
-----
下面继续来说相位谱，下面的图是由七个不同的正弦波叠加构成。相位我们刚刚也说了，表示的是波的状态或者位置，鉴于正弦波是周期性的，我们需要设定一个用来标记正弦波位置的东西。在图中就是小红点，小红点是距离频率轴 $\omega_i = 0$ 最近的波峰。 这些粉色的点只标注了波峰距离频率轴的距离，并不是相位。时间差 $≠$ 相位差，要得到相位还需要乘以 $\frac{2\pi}{T}$ ，如果将一个周期看成是 $2\pi$ 或者 $360°$的话，相位差就是在一个周期内占的比重。
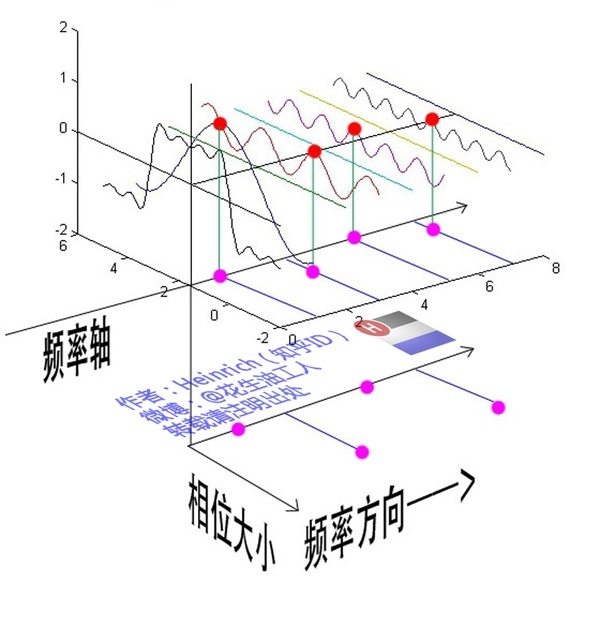
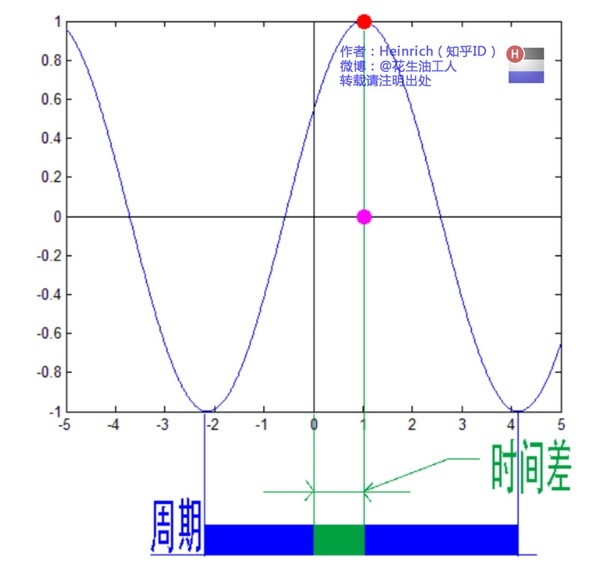
5.2.3 你曾经看过大海吗？关于傅里叶变换的直观理解
刚才都只是谈论离散的频谱图，我们推出来的公式不是连续的吗？那么连续的频谱图应该张成什么样子呢？
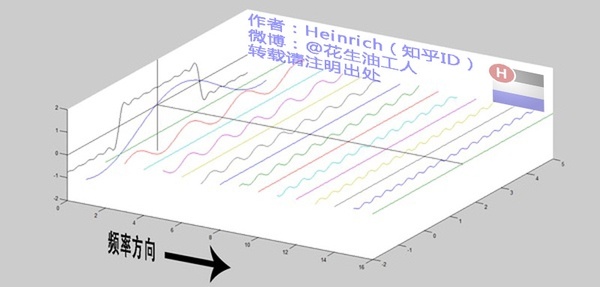
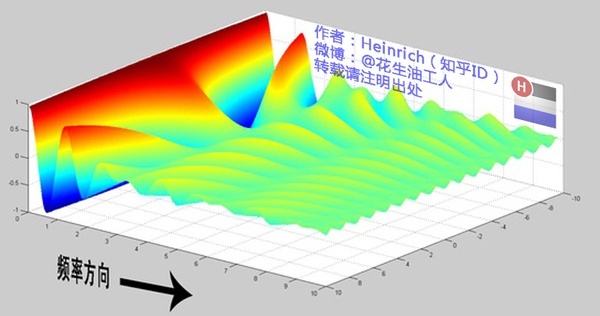
有没有想象出来，就像大海一样。原来离散谱的叠加，变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号，也就是 $\text{5.1.1}$ 的公式的由来。
接下来就是吹嘘时间，我们上面有证明过欧拉公式 $e^{i\theta} = \cos\theta +i\sin\theta \quad \text{(Chapter 4.1)}$ 的正确性。但是谁知道这个优美的公式长成什么样子吗？
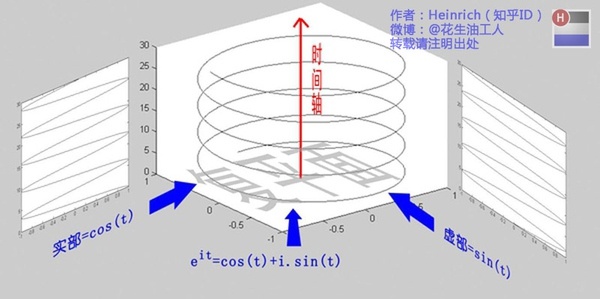
欧拉公式所描绘的，是一个随着时间变化，在复平面上做圆周运动的点，随着时间的改变，在时间轴上就成了一条螺旋线。如果只看它的实数部分，也就是螺旋线在左侧的投影，就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
刚刚我们看过了频谱图的“大海”，却未曾见过复数域下的欧拉公式的“大海”。这个换算回实数域就是频谱图的大海。而其时域就是右边的图。
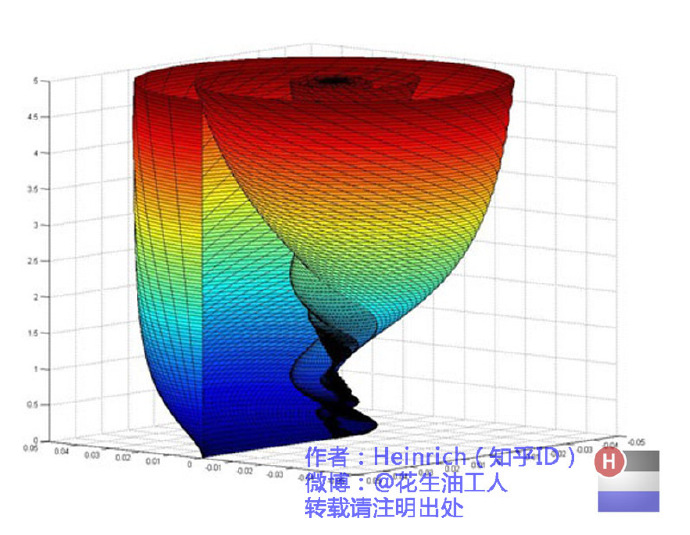<--复频域，时域---></----->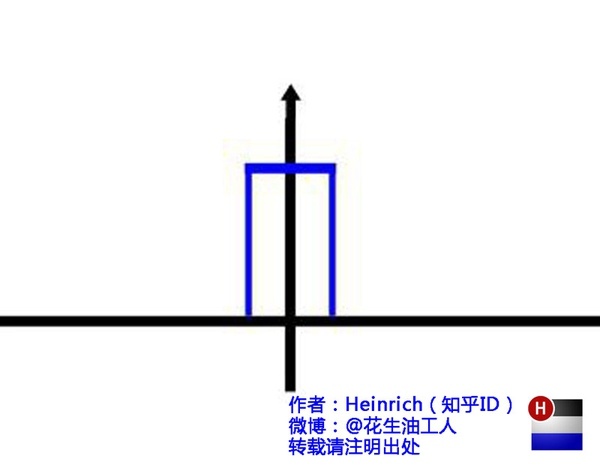
所以我们可以得出傅里叶变换的最终结论：
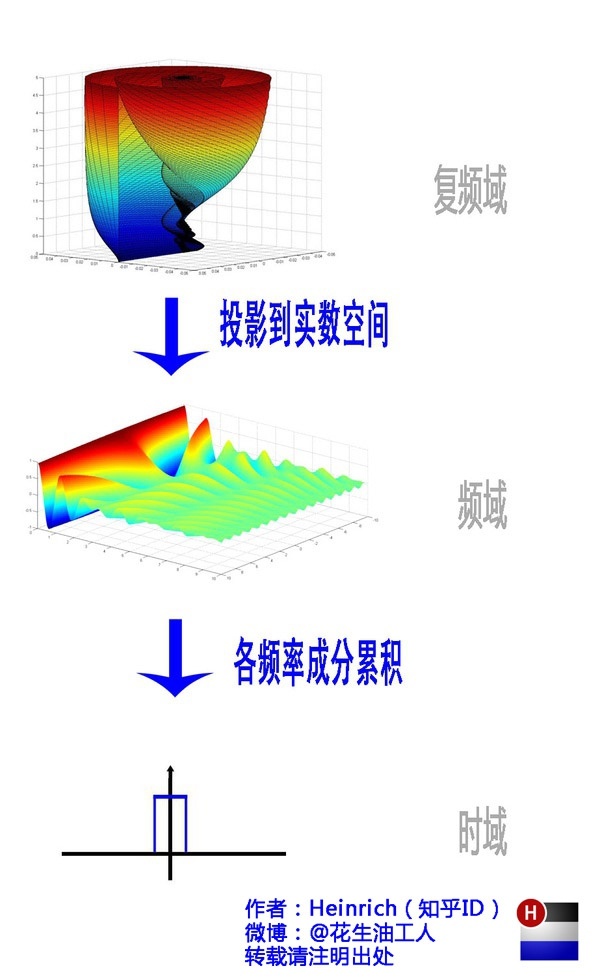
5.2.4 二维图像和频谱图的关系
上图是一个从灰度图通过傅里叶变换得到一个频域图，时域$\rightarrow$ 频域的转换。其中中心最亮的点是频率最低点，往四面八方逐渐变成高频，并且左上-右下是完全对称。其中黑色部分即表明该图像不含有该部分的频率，相反颜色越亮，代表该频率的幅值越高。通常我们会发现中心处是最亮的，即低频信号是最多的，这也和原时域图的信息是匹配的。
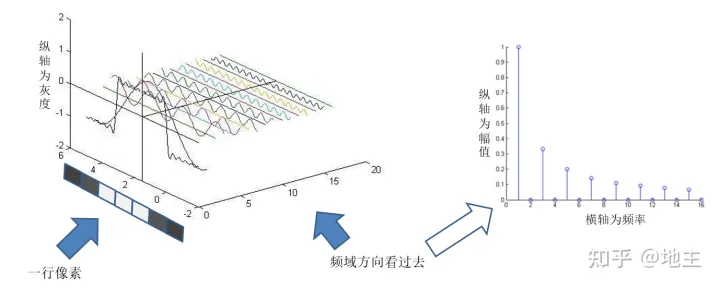
关于频谱图，通常其大小是和原图像一样，但是其$(u,v)$ 坐标却与原图的$(u,v)$ 坐标没有一一对应的关系。
创作等级
会员等级