傅里叶变换FT

傅里叶级数：法国数学家傅里叶发现，任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。

1.三角函数正交性

三角函数正交性用到了：$(i)$三角函数系 $(ii)$ 三角函数的积化和差 $(iii)$ 向量内积

1.1三角函数系

三角函数系就是由下列具有一定规律的正弦函数、余弦函数组成的集合：
$$
0,1,sinx,cosx,sin2x,cos2x,\dots sinnx,cosnx,\dots \tag{1.1.1}
$$
所谓的三角函数的正交性，就是集合中任意两个不同函数乘积在$[-\pi,\pi]$ 上的积分为 $0$。证明需要用到三角函数的积化和差公式。

1.2三角函数的积化和差

$$
sin\theta cos\beta = \frac{1}{2}(sin(\theta +\beta) + sin(\theta - \beta)) \
cos\theta sin\beta = \frac{1}{2}(sin(\beta+\theta) + sin(\beta - \theta)) \
cos\theta cos\beta = \frac{1}{2}(cos(\theta +\beta) + cos(\theta - \beta)) \
sin\theta sin\beta = \frac{1}{2}(cos(\theta -\beta) - cos(\theta + \beta)) \
\tag{1.2.1}
$$

1.3向量内积

假设$\vec{a}=(a_1,a_2,a_3,a_4,\dots,a_n) \quad \vec{b}=(b_1,b_2,b_3,b_4,\dots,b_n)$

如果两个向量正交则：$\vec{a} ·\vec{b} = a_1b_1+a_2b_2+a_3b_3+\dots+a_nb_n = \sum_{i=1}^{n}a_ib_i = 0$

如果将这种正交的概念拓展到函数当中，我们假设$f(x) = a\quad g(x) =b$：$f(x)·g(x) =b\int_{x_0}^{x_1} f(x)g(x)dx = 0$

我们假设$f(x)$和$g(x)$分别是三角函数系中的两个不同的三角函数，则可以证明三角函数的正交性：

2.周期为$2\pi$的傅里叶级数展开

$$
f(x) = \sum_{n=0}^{\infty}(a_n\cos{nx}+b_n\sin{nx}) = a_0 + \sum_{n=1}^{\infty}(a_n\cos{nx}+b_n\sin{nx}) \tag{2.1.1}
\a_0 = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx \quad\quad
a_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos{nx}dx \quad\quad
b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin{nx}dx
$$

证明过程：

2.1 Step1:找$a_0$

我们对$f(x)$求积分：$\int_{-\pi}^{\pi}f(x)dx = \int_{-\pi}^{\pi}{ a_0 }dx + 0 + 0\rightarrow a_0 = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx$

2.2 Step2: :找$a_n$

要想求得 $a_n$ 则需要去除无关变量$a_0$ 和$b_n$ ，根据三角函数正交性，当我们乘以一个 $\cos{nx}$ 的时候$a_0$ 和$b_n$ 项积分之后都是 $0$ ，但是我们得乘以一个 $\cos{mx}$ 使得整个式子更普遍。
$$
\begin{aligned}
\int_{-\pi}^{\pi}f(x)\cos{mx}\space dx &= \int_{-\pi}^{\pi} a_0\cos{mx} dx + \int_{-\pi}^{\pi} \sum_{n=1}^{\infty} a_n\cos{mx}\cos{nx}dx + \int_{-\pi}^{\pi} \sum_{n=1}^{\infty} b_n\sin{nx}\cos{mx}dx \
&=\int_{-\pi}^{\pi}a_n\cos^2{nx}dx + 0 +0 \
&= \int_{-\pi}^{\pi}a_n\frac{1}{2}(1-cos2x)dx \
&= \frac{1}{2}a_n(x - \frac{1}{2}\cos{2x})|^{\pi}{-\pi} = \pi a_n \
&\rightarrow a_n = \frac{1}{\pi}\int{-\pi}^{\pi}f(x)\cos{nx}\space dx \tag{2.2.1}
\end{aligned}
$$

2.3 Step3: :找$b_n$

$b_n$ 的求法和 $a_n$ 的求法相同，在等式两边乘上 $\sin{mx}$ 再求积分，最后我们可以得到 $b_n$：
$$
b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin{nx}\space dx \tag{2.3.1}
$$
至此，证明完毕。

3.周期为$2L$的傅里叶级数展开

3.1利用换元求得一般傅里叶级数

周期为 $2\pi$ 的周期函数 : $f(x) = f(x+2\pi)$ ，同理周期为 $2L$的周期函数 ： $f(t) = f(t+2L)$

原理同周期为$2\pi$的傅里叶级数展开相同，但是我们只需要做一个简单的换元即可求得。我们知道一个周期函数是恒定的，有 $\frac{x}{2\pi} = \frac{t}{2L}$ 。则有 ：$x=\frac{\pi}{L}t$

我们假设 $g(x)$ 为周期为 $2\pi$ 的函数，则$g(x)$ 可以用傅里叶级数展开 :
$$
g(x) = a_0 + \sum_{n=1}^{\infty}(a_n\cos{nx}+b_n\sin{nx})
\a_0 = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx \quad\quad
a_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos{nx}dx \quad\quad
b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin{nx}dx \tag{3.1.1}
$$
我们将 $x=\frac{\pi}{L}t$ 带入到 $g(x)$ 当中 ：

①$x = \pi时\quad t = L$

②$\int_{-\pi}^{\pi}dx\rightarrow\frac{\pi}{L}\int_{-L}^{L}dt$

③$g(\frac{\pi}{L}t) =f(t)= a_0 + \sum_{n=1}^{\infty}(a_n\cos{\frac{n\pi}{L}t}+b_n\sin{\frac{n\pi}{L}t})$
$$
f(t) = a_0 + \sum_{n=1}^{\infty}(a_n\cos{\frac{n\pi}{L}t}+b_n\sin{\frac{n\pi}{L}t})
\a_0 = \frac{1}{2L}\int_{-L}^{L}f(t)dt \quad\quad
a_n = \frac{1}{L}\int_{-L}^{L}f(t)\cos{\frac{n\pi}{L}t}dt \quad\quad
b_n = \frac{1}{L}\int_{-L}^{L}f(t)\sin{\frac{n\pi}{L}t}dt \tag{3.1.2}
$$

3.2将傅里叶级数一般化

时域的表示，时域的横轴是时间，时间无负数 $t>0$ 。则$T = 2L$ 我们记 $\omega = \frac{2\pi}{2L} = \frac{2\pi}{T}$ ，则傅里叶级数可以写成如下形式：

①$\int_{-L}^{L} dt= \int_{0}^{2L} dt= \int_{0}^{T}dt$
$$
f(t) = a_0 + \sum_{n=1}^{\infty}(a_n\cos{n\omega t}+b_n\sin{n\omega t})
\a_0 = \frac{1}{T}\int_{0}^{T}f(t)dt \quad\quad
a_n = \frac{2}{T}\int_{0}^{T}f(t)\cos{n\omega t}dt \quad\quad
b_n = \frac{2}{T}\int_{0}^{T}f(t)\sin{n\omega t}dt \tag{3.2.3}
$$
至此我们已经完成了傅里叶的最基础的求解。但是我们觉得这个公式表达太过于繁杂，在实数域将这个公式简化有点苦难，所以我们引入复数将傅里叶级数公式进一步简化。

4.傅里叶级数的复数展开

4.1欧拉公式证明

我们知道欧拉公式为：$e^{i\theta} = \cos\theta +i\sin\theta$

如果我们要证明这个公式相等，我们可以令 ：$f(x) = \frac{e^{i\theta}}{\cos\theta + i\sin\theta}$

我们对 $f(x)$ 求导 $f’(x) = \frac{ie^{i\theta}(\cos\theta+i\sin\theta)-e^{i\theta}(-\sin\theta + \cos\theta)}{(\cos\theta + i\sin\theta)^2} = \frac{ie^{i\theta}(\cos\theta - \cos\theta)+e^{i\theta}(i\sin\theta-i\sin\theta)}{(\cos\theta + i\sin\theta)^2} = 0$

导数$f’(x) = 0$ 说明 $f(x)$ 是一个常数，我们随便带入一个数来求 $f(x)$ : $f(x) = f(0) = \frac{e^0}{\cos0} = \frac{1}{1} = 1$

说明欧拉公式 $e^{i\theta} = \cos\theta +i\sin\theta$ 成立。

4.2cos、sin复数表示

由欧拉公式的证明可知：不论在什么条件下 ①$e^{i\theta} = \cos\theta +i\sin\theta$ 均成立。

我们将 $-\theta$ 带入到欧拉公式当中 : ②$e^{-i\theta} = \cos(-\theta) +i\sin(-\theta) = \cos\theta-i\sin\theta$

将欧拉公式和上述的 ①和②公式进行联立，可以得到：
$$
\cos\theta = \frac{1}{2}(e^{i\theta}+e^{-i\theta}) \
\sin\theta = -\frac{i}{2}(e^{i\theta}-e^{-i\theta}) \
\tag{4.2.1}
$$

4.3复数形式展开

我们已知傅里叶级数的一般化为：
$$
f(t) = \frac{1}{2}a_0 + \sum_{n=1}^{\infty}(a_n\cos{n\omega t}+b_n\sin{n\omega t})
\a_0 = \frac{2}{T}\int_{0}^{T}f(t)dt \quad\quad
a_n = \frac{2}{T}\int_{0}^{T}f(t)\cos{n\omega t}dt \quad\quad
b_n = \frac{2}{T}\int_{0}^{T}f(t)\sin{n\omega t}dt \tag{3.2.3}
$$
具体的推导过程：
$$
\begin{aligned}
f(x) &= \frac{1}{2}a_0 + \sum_{n=1}^{\infty}(a_n\cos{n\omega t}+b_n\sin{n\omega t}) \
&= \frac{1}{2}a_0 + \sum_{n=1}^{\infty}[\frac{1}{2}a_n(e^{in\omega t}+e^{-in\omega t}) -\frac{i}{2}b_n(e^{in\omega t}-e^{-in\omega t})] \
&= \frac{1}{2}a_0 + \frac{1}{2}\sum_{n=1}^{\infty}[e^{in\omega t}(a_n - ib_n)+e^{-in\omega t}(a_n + ib_n)]\
&= \sum_{n=0}^{0}\frac{1}{2}a_0·e^{in\omega t}+ \sum_{n=1}^{\infty}\frac{1}{2}e^{in\omega t}·(a_n - ib_n) + \sum_{-\infty}^{n=-1}\frac{1}{2}e^{in\omega t}(a_{-n}+b_{-n}) \
&= \sum_{-\infty}^{\infty}C_ne^{in\omega t} \tag{4.3.1}
\end{aligned}
$$
具体的公式已经推导完成，接下来就是讨论$C_n$ 的情况，$C_n$ 的情况有三种 $C_n=\left{
\begin{aligned}
n & =0 & \frac{1}{2}a_0 \
n & >0 & \frac{1}{2}(a_n - ib_n) \
n & <0 & \frac{1}{2}(a_{-n} + ib_{-n})
\end{aligned}
\right.$

①n=0
$$
C_n = \frac{1}{2}a_0 = \frac{1}{T}\int_{0}^{T}f(t)dt = \frac{1}{T}\int_{0}^{T}f(t)e^{-in\omega t}dt \tag{4.3.2}
$$
②n>0
$$
\begin{aligned}
C_n&=\frac{1}{2}(a_n - ib_n) = \frac{1}{2}(\frac{2}{T}\int_{0}^{T}f(t)\cos{n\omega t}dt - \frac{2}{T}\int_{0}^{T}f(t)\sin{n\omega t}dt) \
&= \frac{1}{T}\int_{0}^{T}f(t)(\cos{n\omega t}-i\sin{n\omega t})dt \
&=\frac{1}{T}\int_{0}^{T}f(t)e^{-in\omega t}dt
\tag{4.3.3}
\end{aligned}
$$
②n<0
$$
\begin{aligned}
C_n&=\frac{1}{2}(a_{-n} + ib_{-n}) = \frac{1}{2}[\frac{2}{T}\int_{0}^{T}f(t)\cos{(-n)\omega t}dt + \frac{2}{T}\int_{0}^{T}f(t)\sin{(-n)\omega t}dt] \
&=\frac{1}{T}\int_{0}^{T}f(t)(\cos{n\omega t}-i\sin{n\omega t})dt \
&=\frac{1}{T}\int_{0}^{T}f(t)e^{-in\omega t}dt
\tag{4.3.4}
\end{aligned}
$$
综上：$f(x) = \sum_{-\infty}^{\infty}C_ne^{in\omega t}$ ，$C_n = \frac{1}{T} \int^{T}_{0}f(t)e^{-in\omega t}$

5.傅里叶变换 Fourier Transform

傅里叶级数解决的是周期函数的表达问题，其频谱图是离散的。傅里叶变换解决的是非周期函数的表达问题，其频谱图是连续的。我们上面已经使用一个统一的式子来表达傅里叶级数了，如何将傅里叶级数转换到傅里叶变换，是这一部分的重点内容。这需要一点高数的内容$(i)$ 黎曼和思想 $(ii)$ 频谱图

5.1连续傅里叶变换

假设对于一个周期性的函数 $f(x) = \sum_{-\infty}^{\infty}C_ne^{in\omega t}$ , $C_n = \frac{1}{T} \int^{T}_{0}f(t)e^{-in\omega t}$ ，其函数图像如下： （左：时域图 右：频域图）

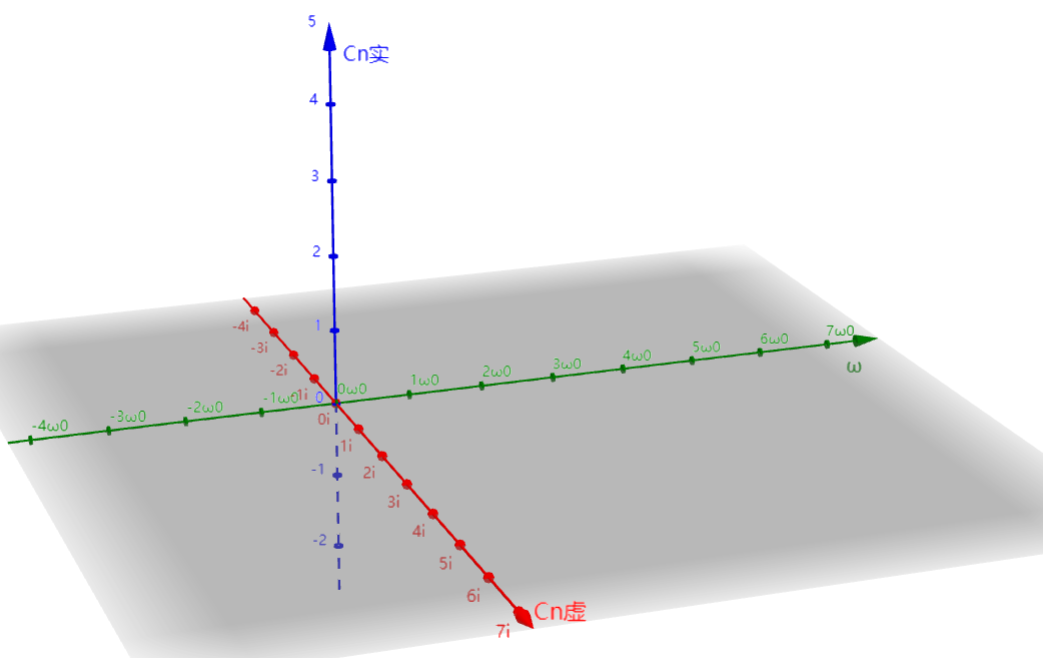
我们记$\omega_0 = \frac{2\pi}{T}$ 记为基频率。

如果我们使用频谱图将傅里叶级数表示出来： $①f(x) = \dots C_{-1}e^{-i\omega t}+C_{0}e^{0}+C_{1}e^{i\omega t}+C_{2}e^{2i\omega t}+\dots$

而$C_n$ 是一个复数，我们可以统一地将其写成： $②a+bi$

通过$①$和$②$便可以画出三维的频谱图像，可以想象得到这个图像是离散的。傅里叶级数我们可以理解成为离散的傅里叶变换。下面是

我们由黎曼和的思想，当周期无限大的时候 $T\rightarrow \infty$ ，$\omega_o = \frac{2\pi}{T} \rightarrow 0^+$上述频谱图的 $\textcolor{red}{n\omega_0}$ 轴的 $\omega_0$ 趋于 $0$ 的时候，频谱图将慢慢变得连续，最终变成一条连续的三维空间的曲线。

对于非周期函数，有：

$①T\rightarrow \infty$ $\rightarrow$ $\lim_{T->\infty}f_T(t) = f(t)$

$②\Delta\omega = (n+1)\omega_0 - n\omega_0 = \omega_0$

$③\Delta\omega = \omega_0 =\frac{2\pi}{T}$ $\rightarrow$ $\frac{1}{T} = \frac{\Delta\omega}{2\pi}$ $\rightarrow$ $\lim_{T->\infty} \Delta\omega \rightarrow 0^{+}$

$④\sum_{n=-\infty}^{\infty} n\omega_0 =\sum_{n=-\infty}^{\infty} n\Delta\omega = \int_{-\infty}^{\infty} d\omega$

然后我们将 $\Delta\omega$ 和 $C_n$ 带入到周期函数 $f_T(t)$ 中：
$$
\begin{aligned}
f_T(t) &= \sum_{-\infty}^{\infty}C_ne^{in\omega t} \
&= \sum_{-\infty}^{\infty}\frac{1}{T} \int^{\frac T 2}{-\frac T 2}f_T(t)e^{-in\omega_0 t}dt \space e^{in\omega_0 t} \
&= \sum{-\infty}^{\infty} \frac{\Delta\omega}{2\pi} \int^{\frac T 2}{-\frac T 2}f_T(t)e^{-in\omega_0 t}dt \space e^{in\omega_0 t} \tag{5.1.1}
\end{aligned}
$$
当$T\rightarrow \infty$ 的时候，我们利用上述已经写好的 $①②③④$条件：
$$
\begin{aligned}
\lim{T\rightarrow\infty} f_T(t) &= f(t) \
&=\frac {1}{2\pi}\int_{-\infty}^{\infty} \int^{\frac T 2}{-\frac T 2}f(t)e^{-i\omega t}dt \space e^{i\omega t} d\omega \
&=\frac {1}{2\pi}\int{-\infty}^{\infty} \int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt \space e^{i\omega t} d\omega \tag{5.1.2}
\end{aligned}
$$
则傅里叶变换（时域到频域）应该为：
$$
F(\omega) = \int_{-\infty}^{\infty} f(t)e^{-i\omega t}dt \tag{5.1.3}
$$
而逆傅里叶变换（频域到时域）则为：
$$
f(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega t}d\omega \tag{5.1.4}
$$

6.文章引用

1.第一期纯干货数学推导傅里叶级数与傅里叶变换Part1三角函数的正交性

2.第二期纯干货数学推导傅里叶级数与傅里叶变换Part2周期为2Pi的函数展开

3.第三期纯干货数学推导傅里叶级数与傅里叶变换Part3周期为2L的函数展开

4.第四期纯干货数学推导傅里叶级数与傅里叶变换Part4傅里叶级数的复数形式

5.第五期纯干货数学推导傅里叶级数与傅里叶变换Part5从傅里叶级数推导傅里叶变换

6.总结篇纯干货数学推导傅里叶级数与傅里叶变换Part6总结与闲话（完)

[7.计算机图形学（第二版） Fundamentals of Computer Graphics ([美] 舍利, Peter Shirley, 高晓春译) (Z-Library)](C:\Users\杨树森\Desktop\PDF WORKSHEET\计算机图形学（第二版） Fundamentals of Computer Graphics ([美] 舍利, Peter Shirley, 高晓春译) (Z-Library) (1).pdf)