4.1卷积
卷积是一种组合，将两个函数通过移动和加权平均得到新的函数，我们记为 $f*g=h$ 。简而言之：加权叠加。
卷积是指在滑动中提取特征的过程，可以形象地理解为用放大镜把每步都放大并且拍下来，再把拍下来的图片拼接成一个新的大图片的过程。CSDN : 卷积的通俗理解
4.1.1一维离散卷积
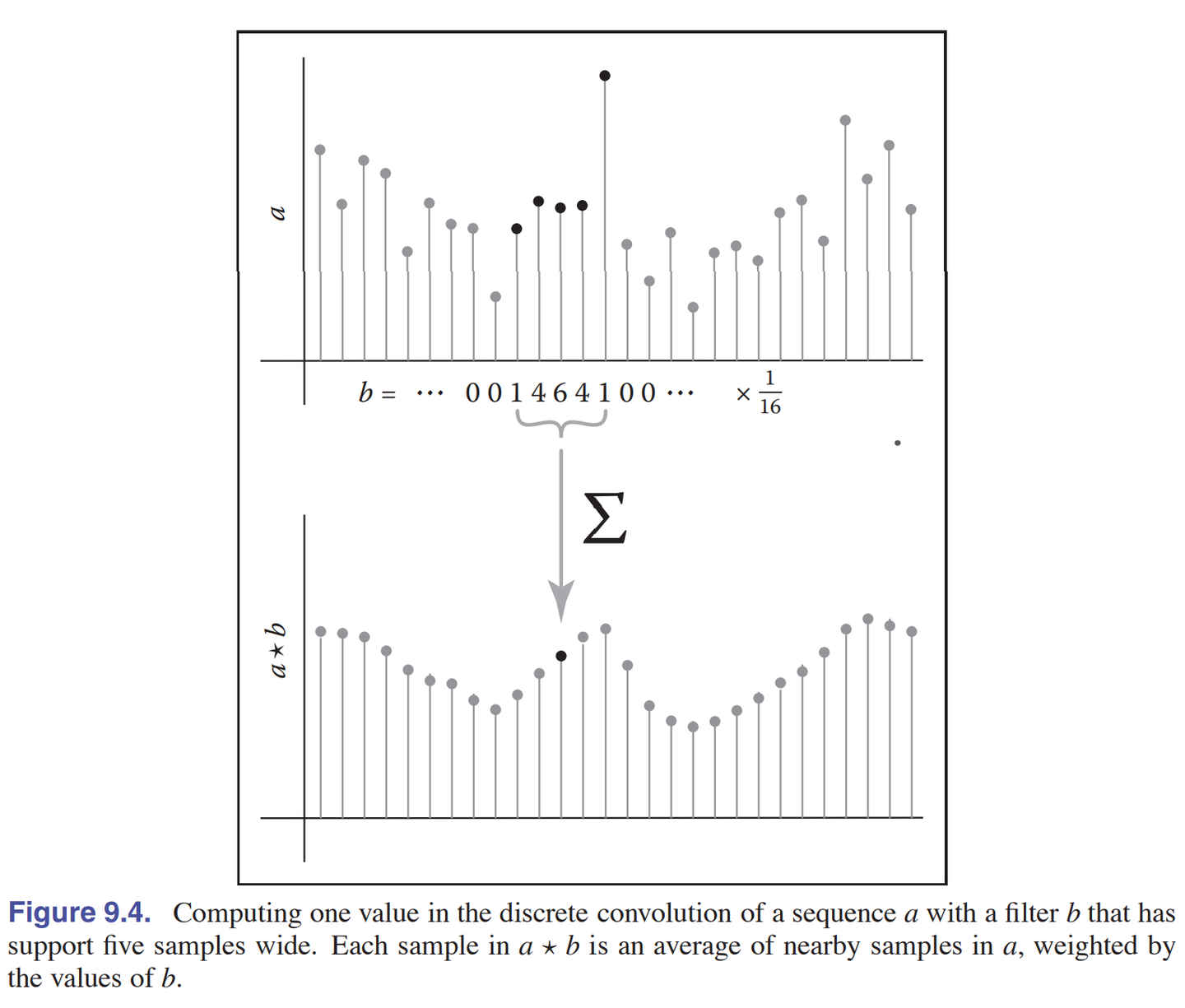
其实我一直都觉得书本这个不太好理解，书本的 $a$ 指的是二维数据，用 $a[i]$ 表示每个二维的点，而 $b$ 则是我们上面说的卷积核（权重矩阵） ，上图的上半部分是原始数据，经过一顿计算：
$\begin{aligned}(ab)[-1]&=\dots +0+a[-3]·b[2]+a[-2]·b[1]+a[-1]·b[0]+a[0]·b[-1]+a[1]·b[-2]+\dots\(ab)[0]&=\dots +0+a[-2]·b[2]+a[-1]·b[1]+a[0]·b[0]+a[1]·b[0]+a[2]·b[-2]+\dots\
(a*b)[1]&=\dots +0+a[-1]·b[2]+a[0]·b[1]+a[1]·b[0]+a[2]·b[0]+a[3]·b[-2]+\dots\end{aligned}$
矩阵理解： $b\Rightarrow{b[-2]=\frac1{16},b[-1]=\frac4{16},b[0]=\frac6{16},b[1]=\frac4{16},b[2]=\frac1{16}}$
理解：假设 $\left{ \begin{aligned} x[0]&=a\quad x[1]=b\quad x[2]=c
\y[0] &= i \quad y[1] = j\quad y[2]=k
\end{aligned} \right.$
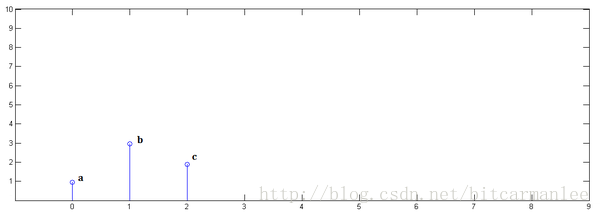
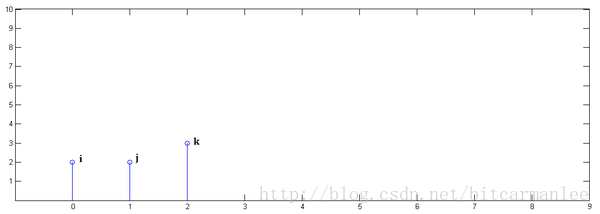
:one: $x[n]$ 乘以$y[0]$并且平移到位置 $0$。 $\Rightarrow i*\begin{pmatrix}a&b&c\end{pmatrix}$
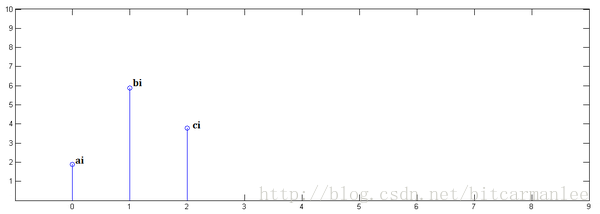
:two: $x[n]$乘以$y[1]$并平移到位置$1$ $\Rightarrow j*\begin{pmatrix}a&b&c\end{pmatrix}$
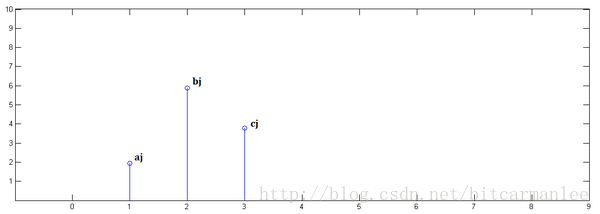
:three: $x[n]$乘以$y[2]$并平移到位置 $2$：$\Rightarrow k*\begin{pmatrix}a&b&c\end{pmatrix}$
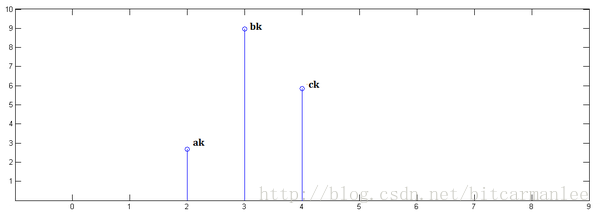
:four: 将上面的三张图片进行叠加，就得到了 $x[n]*y[n]$
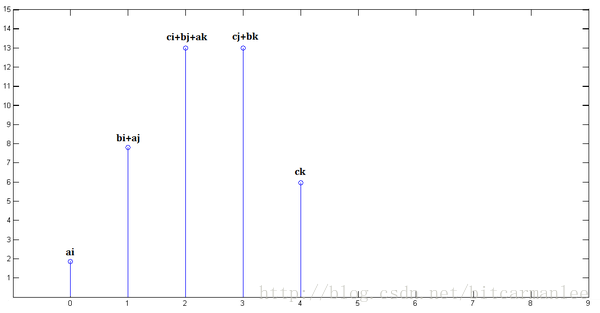
那么书中的卷积就可以理解是 $b$ 有值的部分在数据上进行滑动相乘，卷积就是一个不断前移，不断加权平均的过程。以上卷积操作扩展到$i$ 就是：
$$
(ab)[i]=\sum_{j} a[j]b[i−j] \tag{4.2.1}
$$
$a,b$ 变量走向是相反的，于是可以写成：
$$
(ab)[i]=\sum_{j=i-r}^{i+r} a[j]b[i−j] \tag{4.2.1}
$$
理解：
$$
\begin{aligned}
\text{if} \begin{cases} \text{if\quad origin data:} \quad a = [a_0,a_1,a_2,a_3,\dots,a_n] \
\text{and \quad box filter} \quad b = [b_{-1},b_{0},b_{1}]\end{cases}
\end{aligned}
\Rightarrow
\left { \begin{matrix}
a[0]*b = a_1b_{-1} &a_1b_0 & a_1b_1 \
a[1]*b = &a_2b_{-1} &a_2b_0 &a_2b_1 \
a[2]*b =&&a_3b_{-1} &a_3b_0 &a_3b_1 \
a[3]*b =&&&a_4b_{-1} &a_4b_0 &a_4b_1 \ a[i]*b =&&&& \dots \
a[n-1]*b =&&&&& a_{n}b_{-1}& a_{n}b_0&a_{n}b_1
\end{matrix} \right .
$$
$$
\Rightarrow
\begin{aligned}
\left{\begin{matrix}
&a\ast{b}[0] &=a_1b_1& \
&a\ast{b}[1] &=a_1b_0+a_2b_{-1} \
&a\ast{b}[2] &= a_1b_1+a_2b_0+a_3b_{-1}\
&a\ast{b}[3] &= a_2b_1+a_3b_0+a_4b_{-1}\
&a\ast{b}[4] &= a_3b_1+a_4b_0+a_5b_{-1}\ &\dots &\dots \dots\dots \
&a\ast{b}[i] &= a_{i-1}b_1+a_{i}b_0+a_{i+1}b_{-1} \ &\dots &\dots \dots\dots \
&a\ast{b}[n-1] &= a_{n-2}b_1+a_{n-1}b_0+a_{n}b_{-1}
\end{matrix}\right.
\end{aligned} \Rightarrow a\ast{b}[i] = \sum_{j=i-r}^{i+r}a_jb_{i-j}#
$$
为什么 $b$ 的下标是 $(i-r)?$ 我们将 $j=i-r$ 代入进去 ，可以得到 $i-j = i-r$ 到 $i+r$ ，恰好是一个 box - filter 的长度。
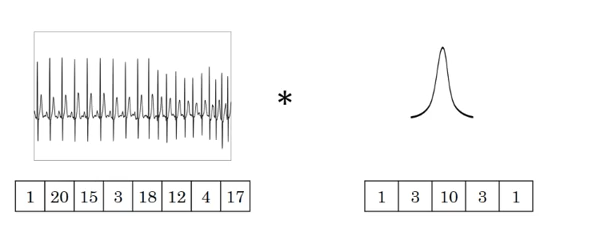
图中的输入的数据维度为8，过滤器的维度为5。与二维卷积类似，卷积后输出的数据维度为: $8-5+1=4$
其应该输出： $[1,23, 85, 251, 238, 161, 244, 206, 145, 194, 55, 17]$
当$|k|>2$时$b[k]=0$，2称为过滤器 $b$ 的半径，其中随着 $j$ 的变化。可以把卷积中的被卷积函数看作输入，而过滤器是卷积的参数，所以卷积的效果完全取决于选择了什么过滤器。一种常见的过滤器是箱式过滤器(bof-filter)，它其实就是求平均值：
$$
b[k]=\left{ \begin{aligned}& \frac{1}{2r+1} \quad &-r<k<r
\&0\quad &others
\end{aligned} \right. \tag{4.2.2}
$$
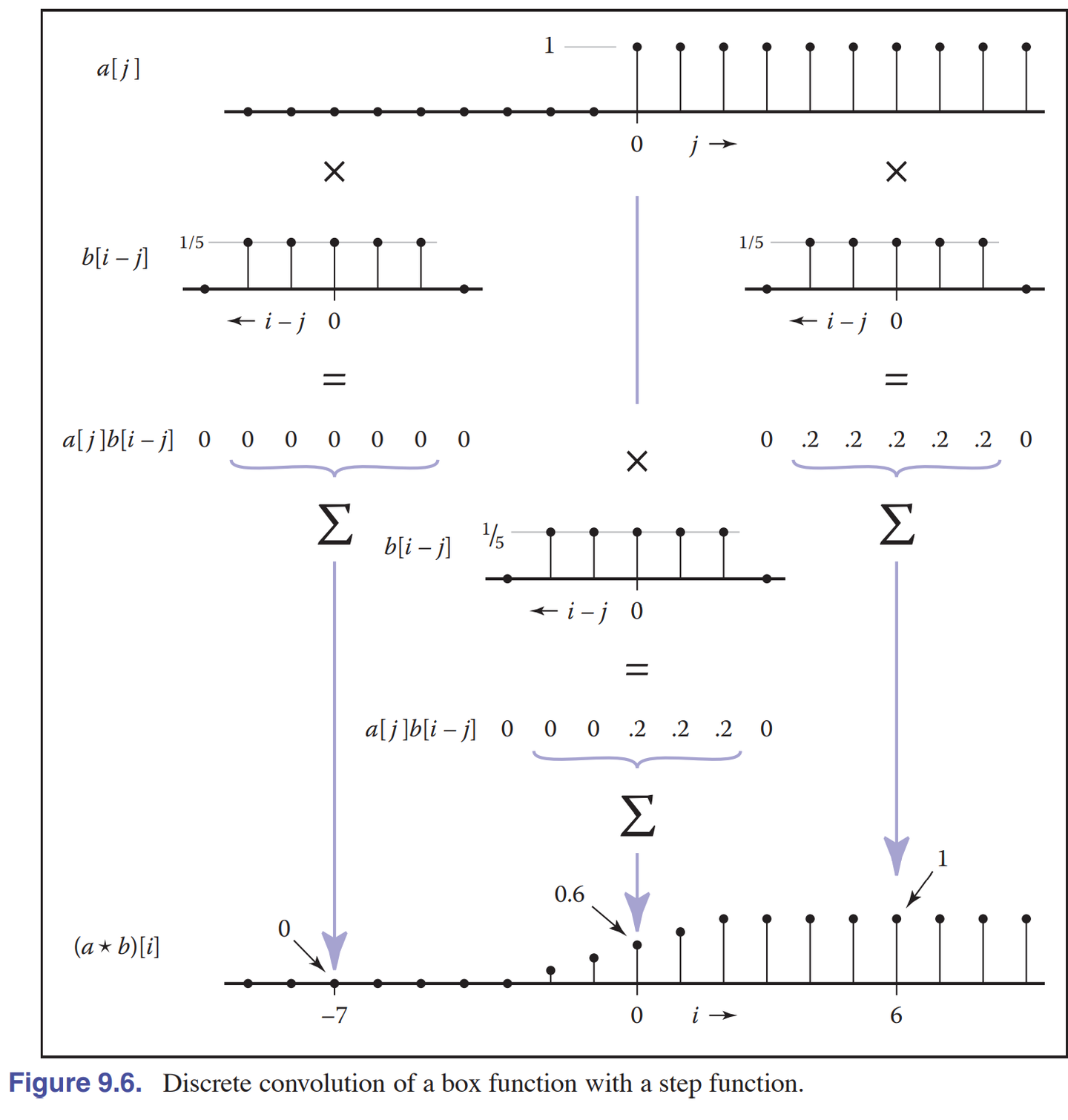
上图可以用加权叠加的思想来解释，$b$ 从数据的最左边开始滑动，得到中间图$1$ ，向右边滑动，得到中间图$2$ ，重复直至完全到数数据末尾。可以看到原函数在$i=0$处的剧烈变化在卷积之后被抚平了，而在远离$i=0$的两端，卷积得到的函数的图像和原函数一致。
4.1.2高维离散卷积
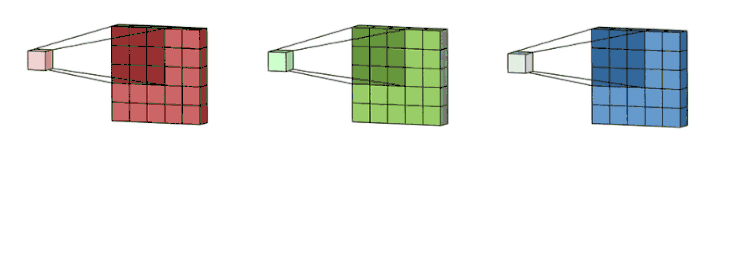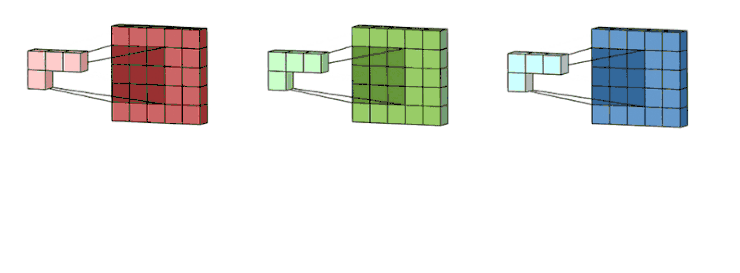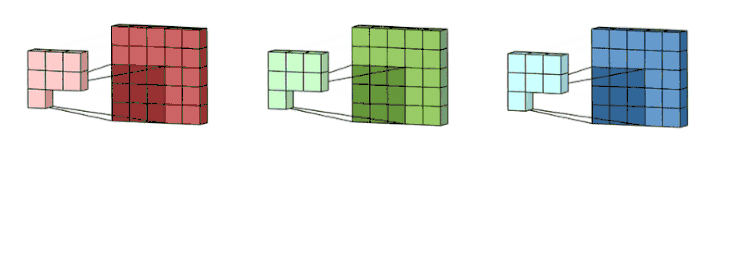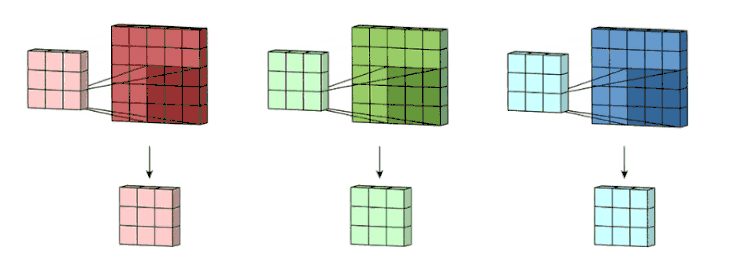
先从最简单的二维卷积开始： 让一个卷积核（权重矩阵）逐步在二维数据上扫描，卷积核滑动的同时，计算权重矩阵和扫描所得到的的数据矩阵的乘积，将结果汇总输出一个像素。卷积核越小，输入输出的位置越接近；卷积核越大，距离就越远。这里所谓的距离指的是合并特征的多少。 我们可以用一张更加生动形象的动图来展示卷积计算的过程。
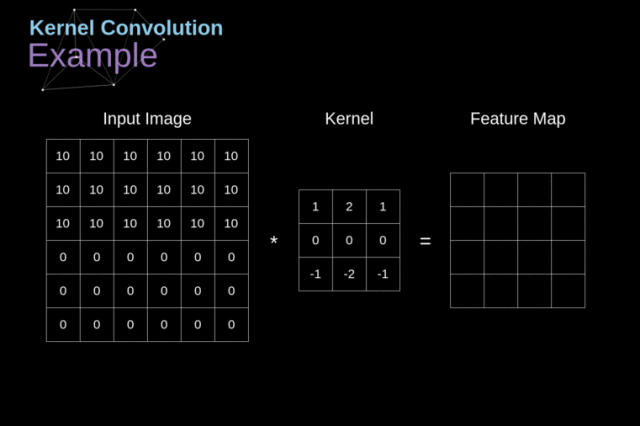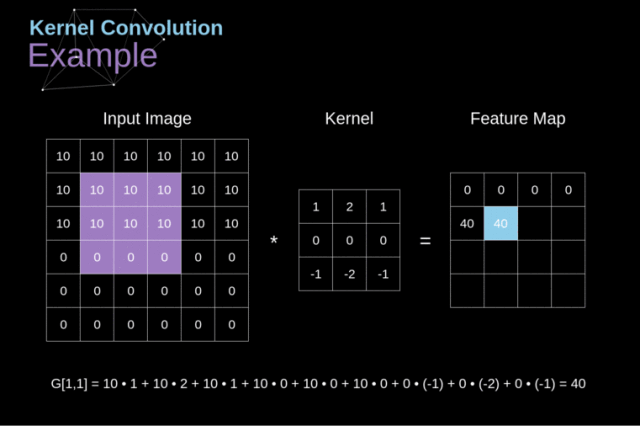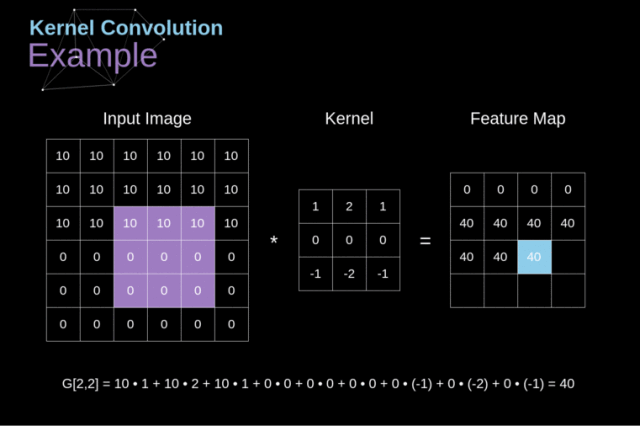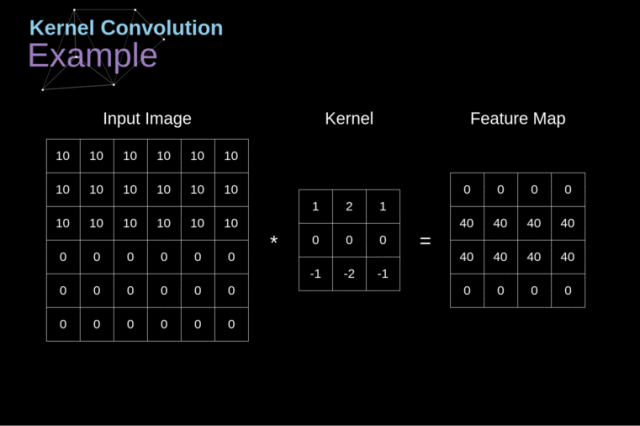
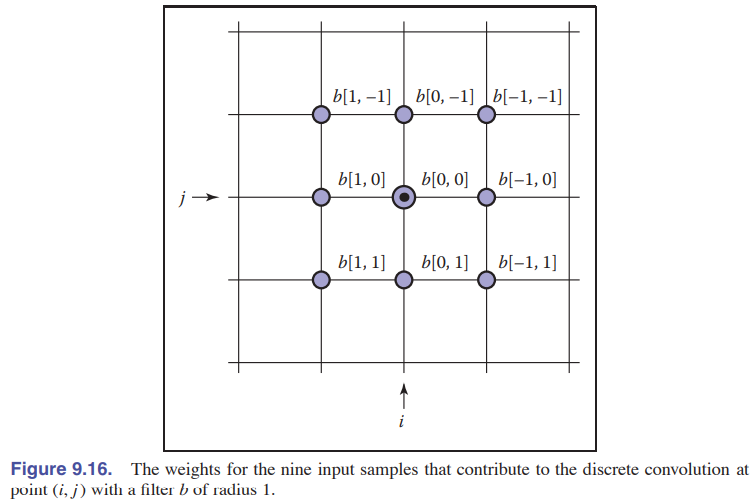
从一维卷积到二维卷积，本质不变，过滤器在原数据上采样并得到新的像素值，其公式为：
$$
\begin{aligned}
(a\ast{b})[i,j]&=\sum_{i’}\sum_{j’}a[i’,j’]b[i-i’,j-j’] \
&=\sum_{i’=i-r}^{i+r}\sum_{j’=j-r}^{j+r}a[i’,j’]b[i-i’,j-j’]
\end{aligned} \tag{4.2.3}
$$
连续函数的二维卷积：
$$
\begin{aligned}
(f\ast g)(x,y)&=\iint{f(x{‘},y{’})g(x-x{‘},y-y{’})dx{‘}dy{’}}\
\end{aligned}
$$
4.1.3连续卷积的理解
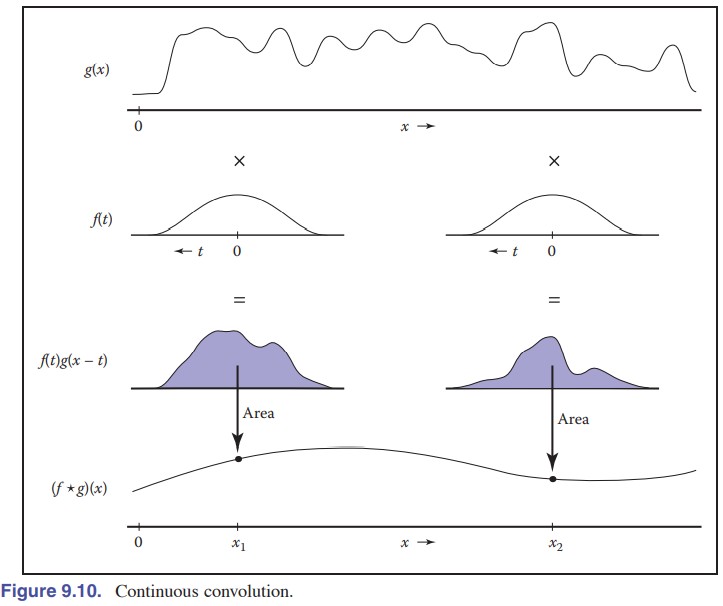
连续区间上的求和就是积分，因此其卷积为：$(f(\tau)\ast g(\tau))(t) = \int_{\tau = -\infty}^{\tau = \infty}f(\tau)g(t-\tau)d\tau \Rightarrow (f\ast g)(t)$
通俗的理解是，原函数$f$ 与过滤器 $g$相乘得到的曲线与$x$ 轴围城的面积。
关于如何将连续的卷积写成离散的卷积，具体可以查看：史上最全的卷积性质及其证明！(共10条)
4.1.4卷积的性质
我们先引入离散和连续卷积的定义：
连续卷积：$(f(\tau)\ast g(\tau))(t) = \int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau.$
离散卷积：$(a*b)[\tau]=\sum_{t} a[\tau]b[\tau−t]$
性质:one: : 交换律： $(f(\tau)\ast g(\tau))(t) = (g(\tau)\ast f(\tau))(t) $
-
- 写出原式： $(f(\tau)\ast g(\tau))(t) = \int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau.---------①$
- 做换元：$t- \tau:= \xi\Rightarrow \tau = t-\xi\Rightarrow d\tau= d(t-\xi)=d(-\xi),\tau=-\infty\Rightarrow \xi=+\infty \Rightarrow \tau=+\infty\Rightarrow \xi=-\infty.—②$
- 换元后得到： $\int_{\xi=+\infty}^{\xi=-\infty}f(t-\xi)g(\xi)(-d\xi) = \int_{\xi=-\infty}^{\xi=+\infty}f(t-\xi)g(\xi)d\xi. -------③$
- 令$\xi:=\tau$ ，有：$\int_{\xi=-\infty}^{\xi=+\infty}f(t-\xi)g(\xi)d\xi = \int_{\tau=-\infty}^{\tau=+\infty}f(t-\tau)g(\tau)d\tau.-------④$
- $(g(\tau)\ast f(\tau))(t) = \int_{\tau=-\infty}^{\tau=+\infty}f(t-\tau)g(\tau)d\tau.# ------⑤$
性质:two: : 分配律：$f(\tau)\ast (g(\tau)+h(\tau))(t) = f(\tau)\ast h(\tau)(t)+f(\tau)\ast g(\tau)(t)$
-
- 将上述左边式子展开： $\begin{aligned}
&f(\tau)\ast (g(\tau)+h(\tau))(t) \
&=\int_{-\infty}^{\infty} f(\tau)·(g(t-\tau)+h(t-\tau))dr \
&= \int_{-\infty}^{\infty} f(\tau)·g(t-\tau)dr+\int_{-\infty}^{\infty} f(\tau)·h(t-\tau)dr .
\end{aligned} -------①$ - 再将其合并成标准的卷积的式子： $\Rightarrow (f(\tau)\ast g(\tau))(t)+(f(\tau)\ast h(\tau))(t)# ------②$
- 将上述左边式子展开： $\begin{aligned}
性质 :three: : 结合性：$(((f(\xi)\ast g(\xi))(\tau))\ast h(\tau))(t) = (f(\tau)\ast ((g(\xi)*h(\xi))(\tau)))(t)$
-
- 将上述左边式子展开： $\begin{aligned}
&(((f(\xi)\ast g(\xi))(\tau))\ast h(\tau))(t) \
&=\int_{\tau= -\infty}^{\tau =\infty} (
\int_{\xi= -\infty}^{\xi=\infty}f(\xi)·g(\tau -\xi) d\xi) ·h(t-\tau)d\tau \
&= \int_{\xi= -\infty}^{\xi=\infty}f(\xi) (
\int_{\tau= -\infty}^{\tau =\infty}g(\tau -\xi)·h(t-\tau)d\tau) d\xi.
\end{aligned} --------①$ - 换元：$\tau-\xi:=\kappa \Rightarrow d\kappa =d\tau\Rightarrow \tau=±\infty,\kappa=\tau-\xi=±\infty --------②$
- $①$式换元之后可得： $\begin{aligned} \end{aligned}$ $\begin{aligned}
&\int_{\xi= -\infty}^{\xi=\infty}f(\xi) (
\int_{\tau= -\infty}^{\tau =\infty}g(\tau -\xi)·h(t-\tau)d\tau) d\xi \
&=\int_{\xi= -\infty}^{\xi=\infty}f(\xi) (
\int_{\kappa= -\infty}^{\kappa =\infty}g(\kappa)·h(t-(\xi+\kappa))d\kappa)d\xi\
&=\int_{\xi= -\infty}^{\xi=\infty}f(\xi) (
\int_{\kappa= -\infty}^{\kappa =\infty}g(\kappa)·h((t-\xi)-\kappa)d\kappa)d\xi \ &=\int_{\xi= -\infty}^{\xi=\infty}f(\xi) ( (g(\kappa)\ast h(\kappa))(t-\xi) )d\xi
\end{aligned} --------③$ - 再进行换元：$\xi;=\tau,\kappa:=\xi \Rightarrow d\xi=d\tau,d\kappa=d\xi -----④$
- $③$式换元之后可得：$\begin{aligned}
&\int_{\xi= -\infty}^{\xi=\infty}f(\xi) ( (g(\kappa)\ast h(\kappa))(t-\xi) )d\xi \
&=\int_{\tau= -\infty}^{\tau=\infty}f(\tau) ( (g(\xi)\ast h(\xi))(t-\tau) )d\tau
\end{aligned} ----- ⑤$ - 定义：$(g(\xi)\ast h(\xi))(t-\tau)= a(t-\tau) \Rightarrow ⑤:\int_{\tau= -\infty}^{\tau=\infty}f(\tau)(a(t-\tau)) d\tau ----------⑥$
- 由$⑥$有 $\int_{\tau= -\infty}^{\tau=\infty}f(\tau)(a(t-\tau)) d\tau = (f(\tau)\ast a(\tau))(t) \Rightarrow (f(\tau)\ast ((g(\xi)*h(\xi))(\tau)))(t) -----⑦$
- 将上述左边式子展开： $\begin{aligned}
性质4 : 与单位脉冲分布(Dirac 脉冲)的卷积 : $(f(\tau)\ast \delta(\tau-t_0))(t) = f(t-t_0)$
脉冲函数，用于描述瞬间或空间几何点上的物理量。脉冲函数也称为$\delta$ 函数，若在一维空间中，自变量为时间 $t$ 的函数 $\delta(t)$ ，满足下述两个条件：$①\delta(t)= \begin{cases} +\infty,\quad t=0\0,\quad \quad \space t≠0\end{cases} $ $②\int_{-\infty}^{+\infty}{\delta(t)\space dt}=1$ 的函数称为$\delta$ 函数。
$\delta$ 函数有以下述关系式：$\int_{a}^{b}{\delta(t)} = \begin{cases} 1,a<0<b\0,\quad others \end{cases}$
脉冲函数性质：
-
$\delta$ 函数为偶函数：$\delta(t) = \delta(-t)$
-
设$f(t)$是定义在实数域上的有界函数（$abs(f(t))≤M$），且在$t_0$处连续，则: $\int_{-\infty}^{\infty}\delta(t-t_0)f(t)\space dt = f(t_0)$
-
如果$t_0 = 0$ ，则有：$\int_{-\infty}^{\infty}\delta(t)f(t)\space dt = f(0)$
证明如下
-
-
由性质二的交换律可以得到： $(f(\tau)\ast \delta(\tau-t_0))(t) = (\delta(\tau-t_0) \ast f(\tau) )(t) -------①$
-
由连续卷积和$\delta$ 函数性质二的定义： $\begin{aligned}
&(\delta(\tau-t_0) \ast f(\tau) )(t) \
&=\int_{-\infty}^{\infty}\delta(\tau-t_0)·f(t-\tau)d\tau \
&=\int_{-\infty}^{\infty}\delta(\tau-t_0)·f(t-t_0)d\tau \
&=f(t-t_0) \int_{-\infty}^{\infty}\delta(\tau-t_0)d\tau \
&=f(t-t_0)
\end{aligned} -----②$ -
当 $t_0 = 0$ 时：$(f(\tau)\ast \delta(\tau-t_0))(t) = f(t)$
-
4.1.5卷积的边界处理
在处理边缘的值的时候，我们需要补充新的值，有以下几种处理办法：
- 扩展(extern)：将边缘的值扩展r个长度
- 重复(wrap)：取另一边的值，比如在右边卷积时，直接来到左边取缺少的值
- 镜像(mirror)：想象在边缘放上一面镜子，那么在信号之外的值可以在信号内的对称位置找到
- 裁剪(crop)：在缺少值的位置选择不卷积，因此卷积结果会比输入要小一圈
- 常量(constant)：使用一个固定的值补全所有缺少的值
- 重正化(renormalization)：只选取边界以内的值进行计算，最后对结果进行正规化（保留原函数的趋势）
4.2卷积滤波器
4.2.1常用的过滤器[一维]
我们所有的过滤器都以连续的形式给出，对连续形式的过滤器在整数集上采集就可以得到离散版本。
① : 箱式过滤器
$$
b[k]=\left{ \begin{aligned}& \frac{1}{2r+1} \quad &-r<k<r
\&0\quad &others
\end{aligned} \right. \tag{4.2.3}
$$
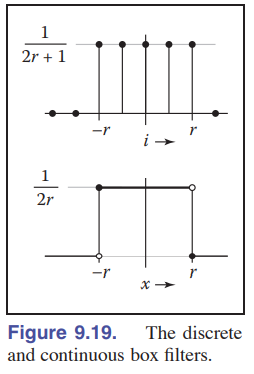
其实我们在前面介绍一维卷积的时候就已经说过了，其中半径 $r$ 是箱式过滤器的参数，注意到连续版本的箱式过滤器中 $x$ 不取到 $x=r$ ，否则结果就可能因为多取了值而产生偏差。
box filter 官方API
#include <iostream>
#include <opencv2/opencv.hpp>
#include <iostream>
#include <ctime>
#include <string>
using namespace std;
using namespace cv;
int main(void) {
clock_t time_beg = 0;
clock_t time_end = 0;
std::string path = "C:\\Users\\杨树森\\Desktop\\2.jpg";
cv::Mat image = cv::imread(path,cv::IMREAD_UNCHANGED);
image.convertTo(image,CV_32FC3); //CV_32F:5; CV_32FC3:CV_MAKETYPE(CV_32F,3)
image /= 255.0f;
int radius = 9;
int kernal_size = radius * 2 + 1;
cv::Mat image_box_filter_cv; //OpenCV 自带的box滤波
cv::boxFilter(image, image_box_filter_cv,-1,cv::Size(kernal_size,kernal_size),
cv::Point(-1,-1),true,cv::BORDER_CONSTANT);
time_end = clock();
std::cout << "box-filter-cv time cost: " << time_end - time_beg << std::endl;
cv::namedWindow("original_image", 1);
cv::imshow("original_image", image);
cv::namedWindow("cv_box_filter", 1);
cv::imshow("cv_box_filter", image_box_filter_cv);
cv::waitKey(0);
cv::destroyAllWindows();
}
box filter 暴力实现
我们之前学过一维的卷积为 $a\ast{b}[i] = \sum_{j=i-r}^{i+r}a[j]b[i-j]$ ，二维卷积为 $a\ast{b}[i.j] = \sum_{\hat{i}=i-r_1}^{i+r_1}\sum_{\hat{j} = j - r_2}^{j+r_2}a[\hat{i},\hat{j}]b[i-\hat i,j-\hat j]$
box filter 的作用很简单，就是对全局区域求平均(没有 $b$)，并将某个值赋给某个点，一般我们赋给区域中心。用公式表达如下：
$$
result(row,column)=\frac1{n^2}\sum_{i=col-radius_1}^{col+radius_1}\sum_{j=row-radius_2}^{row+radius_2} image{(i,j)} \tag{box filter}
$$
其中 $patch$ 是以$(row,column)$ 为重心的一块区域。为了和后面的公式对应上， 我们还需对我们的公式的做些定义，稍加限制：
:small_red_triangle:$ r:$ $patch$ 的半径。半径在宽高方向可以不相等，我们以理解为目的，将其设置为相等。
$n:pitch$ 的长度，等于$2*r+1$ 。
$(rows,cols)$：图像的尺寸，行数和列数。
$(row,col):$ 对应图像的索引。
$(i,j):$ 对应 $patch$ 的索引。
$k:$对应通道的索引。
cv::Mat BoxFilter_1(const cv::Mat &image,int radius) {
int cols = image.cols , //cols: image height
rows = image.rows; //rows: image width
int channels = image.channels(); //RGBA Channels
int col_bound = cols - 1, //max-index of height and width
row_bound = rows - 1;
cv::Mat result(rows, cols, CV_32FC3); //CV_32FC32 : 32 bit float type
clock_t time_beg = clock();
clock_t time_end = NULL;
for(int row = 0; row < rows; row++){
int row_beg = cv::max(row - radius, 0);
int row_end = cv::min(row + radius, row_bound);
for (int col = 0; col < cols; col++) {
int col_beg = cv::max(col - radius, 0);
int col_end = cv::min(col + radius, col_bound);
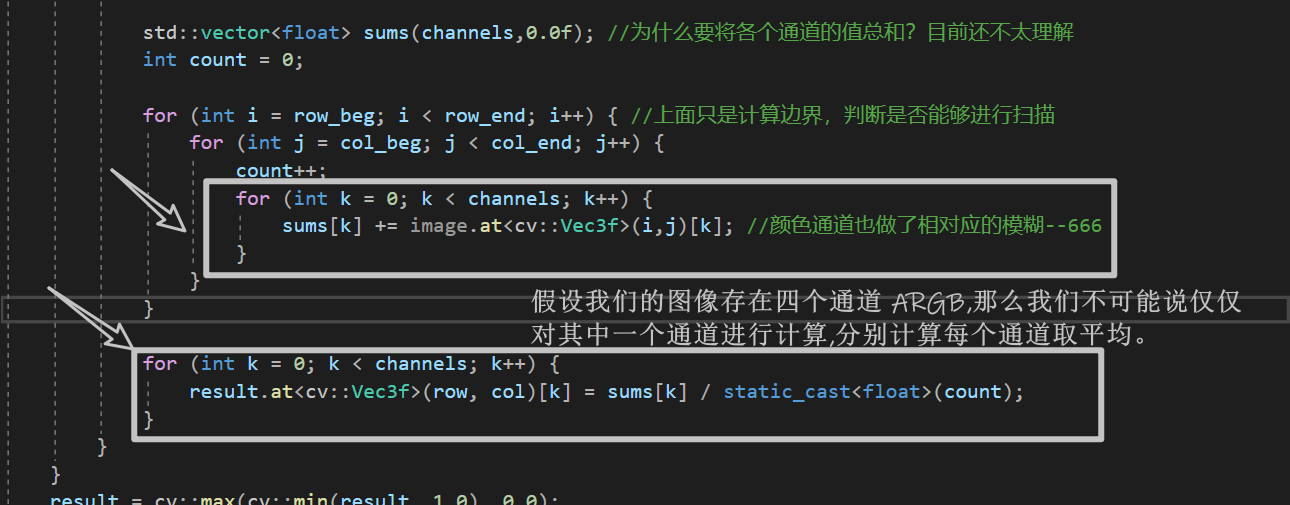
std::vector<float> sums(channels,0.0f); //为什么要将各个通道的值总和？目前还不太理解
int count = 0;
for (int i = row_beg; i < row_end; i++) { //对单个patch进行卷积操作
for (int j = col_beg; j < col_end; j++) {
count++;
for (int k = 0; k < channels; k++) {
sums[k] += image.at<cv::Vec3f>(i,j)[k]; //我们使用的是 box-filter 就是将其傻傻加到一起
}
}
}
for (int k = 0; k < channels; k++) {
result.at<cv::Vec3f>(row, col)[k] = sums[k] / static_cast<float>(count);
}
//到这里我们已经完成了单个像素的卷积操作，使用到的过滤器是 box-filter
}
}
result = cv::max(cv::min(result, 1.0), 0.0); //确保像素值在[0,1],不会越界
time_end = clock();
std::cout << "box-filter-1 time cost: " << time_end - time_beg << std::endl;
return result;
}
代码中的 row_beg 、row_end 以及 col_beg、col_end 分别对应了上述公式中的 $i=col-radius,col+radius$ ,$j = row-radius,row+radius$
:pig_nose: 补充知识：:one: : OpenCV 基本 API 概念：Mat 类是存储和操作 OpenCV 中图像的主要数据结构。这个类是在 core 模块中定义的。OpenCV 已经实现了对于这些数据结构自动分配和释放内存的机制。OpenCV教程：超详细的OpenCV入门教程，值得收藏
:pig_nose: 补充知识：:two: ：所谓的二维就是两个一维度的相乘罢了， 我们之前也讲过一维的计算： 加权叠加。
box filter 行列分离
$pitch$ 的平均可以进行行列分离：
对于每一行，我们遍历该 $row$ 中的所有像素，并计算该像素周围半径为 $radius_1$ 像素的平均值，讲这个值给缓存下来row_result 。
对于每一列，我们遍历该 $column$ 中的所有像素，并计算该像素周围半径为 $radius_2$ 像素的平均值，将最终相加结果赋给result 。
$$
\frac{1}{n^2}\sum_i\sum_j{image(i,j)}=\frac1n\sum_i\frac1n\sum_j{image(i,j)} \tag{box filter optimize 01}
$$
cv::Mat BoxFilter_2(const cv::Mat& image, int radius) {
int cols = image.cols,
rows = image.rows;
int channels = image.channels();
int col_bound = cols - 1,
row_bound = rows - 1;
cv::Mat result(rows,cols,CV_32FC3);
cv::Mat row_result(rows, cols, CV_32FC3);
clock_t time_beg = clock();
clock_t time_end = NULL;
/*compute mean for row-wise*/
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
int col_beg = cv::max(col - radius,0);
int col_end = cv::min(col + radius, col_bound);
std::vector<float> sums(channels, 0.0f);
int count = 0;
for (int j = col_beg; j < col_end; j++) {
count++;
for (int k = 0; k < channels; k++) {
sums[k] += image.at<Vec3f>(row, j)[k];
}
}
for (int k = 0; k < channels; k++) {
row_result.at<cv::Vec3f>(row, col)[k] = sums[k] / static_cast<float>(count);
}
}
}
/*compute mean for col-wise*/
for (int col = 0; col < cols; col++) {
for (int row = 0; row < rows; row++) {
int row_beg = cv::max(row - radius, 0);
int row_end = cv::min(row + radius, row_bound);
std::vector<float> sums(channels, 0.0f);
int count = 0;
for (int i = row_beg; i < row_end; i++) {
count++;
for (int k = 0; k < channels; k++) {
sums[k] += row_result.at<Vec3f>(i, col)[k];
}
}
for (int k = 0; k < channels; ++k) {
result.at<Vec3f>(row, col)[k] = sums[k] / static_cast<float>(count);
}
}
}
result = cv::max(cv::min(result,1.0),0.0);
time_end = clock();
std::cout << "box-filter-2 time cost: " << time_end - time_beg << std::endl;
return result;
}
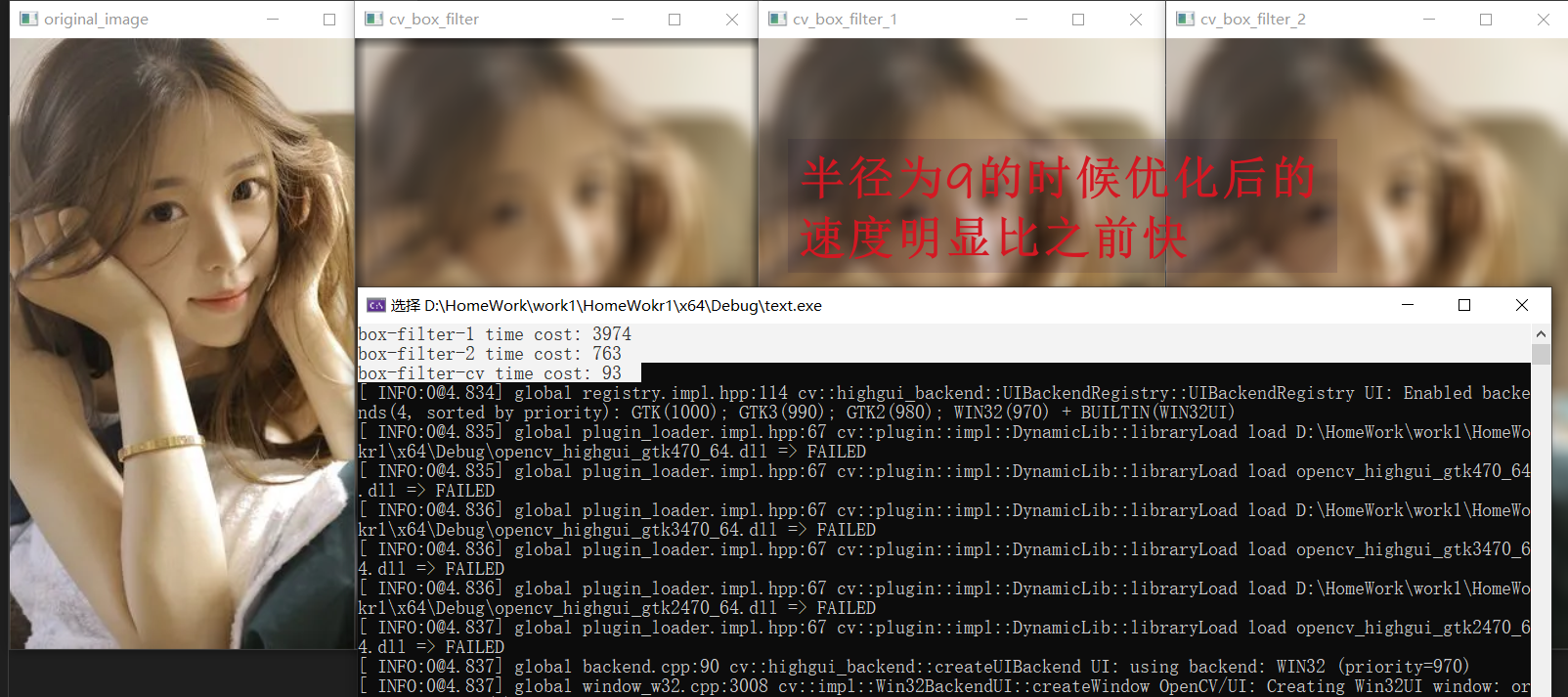
box filter行列分离优化
cv::Mat BoxFilter_3(const Mat& image, int radius)
{
int cols = image.cols;
int rows = image.rows;
int channels = image.channels();
cv::Mat result(rows, cols, CV_32FC3);
clock_t time_beg;
clock_t time_end;
time_beg = clock();
// compute mean for row-wise
cv::Mat row_result(rows, cols, CV_32FC3);
for (int row = 0; row < rows; ++row) {
// initialize sums for row
std::vector<float> sums(channels, 0.0f);
int count = 0;
for (int col = 0; col < radius; ++col) { //单个像素卷积 - begin
if (col < cols) {
count++; // count = radius
for (int k = 0; k < channels; ++k) {
sums[k] += image.at<cv::Vec3f>(row, col)[k];
} //单个像素相加完成
}
}
// process row
for (int col = 0; col < cols; ++col) {
int left = col - radius - 1;
int right = col + radius;
if (left >= 0) { //判断左边是否没有越界
count--; //如果左边界没有越界，那么就说明左边还有像素可以用来计算平均值，否则就不能再往左计算平均值了。
for (int k = 0; k < channels; ++k) {
sums[k] -= image.at<cv::Vec3f>(row, left)[k];
}
}
if (right < cols) { //判断有边界是否有越界
count++;
for (int k = 0; k < channels; ++k) {
sums[k] += image.at<cv::Vec3f>(row, right)[k];
}
}
for (int k = 0; k < channels; ++k) {
row_result.at<cv::Vec3f>(row, col)[k] = sums[k] / static_cast<float>(count);
}
}
}
// compute mean for column-wise
for (int col = 0; col < cols; ++col) {
// initialize sums for column
vector<float> sums(channels, 0.0f);
int count = 0;
for (int row = 0; row < radius; ++row) {
if (row < rows) {
count++;
for (int k = 0; k < channels; ++k) {
sums[k] += row_result.at<Vec3f>(row, col)[k];
}
}
}
// process column
for (int row = 0; row < rows; ++row) {
int up = row - radius - 1;
int down = row + radius;
if (up >= 0) {
count--;
for (int k = 0; k < channels; ++k) {
sums[k] -= row_result.at<Vec3f>(up, col)[k];
}
}
if (down < rows) {
count++;
for (int k = 0; k < channels; ++k) {
sums[k] += row_result.at<Vec3f>(down, col)[k];
}
}
for (int k = 0; k < channels; ++k) {
result.at<cv::Vec3f>(row, col)[k] = sums[k] / static_cast<float>(count);
}
}
}
result = cv::max(cv::min(result, 1.0), 0.0);
time_end = clock();
cout << "box-filter-3 time cost: " << time_end - time_beg << endl;
return result;
}
这段代码和之前的两段代码可以说是几乎完全不同。我们以 row-wise 为例，if (left >= 0) 和 if(right < cols) 这两个使用来确定我们要进行计算的col的边界。为什么要使用两个if 来确定边界？ 因为使用 row_beg,row_end 等还需要进行循环计算，使得复杂度大大升高，所以我们引入两个 if 来计算边界会快很多。所以你会发现其实上述代码少了row_bound,col_bound ，因为用不到了。
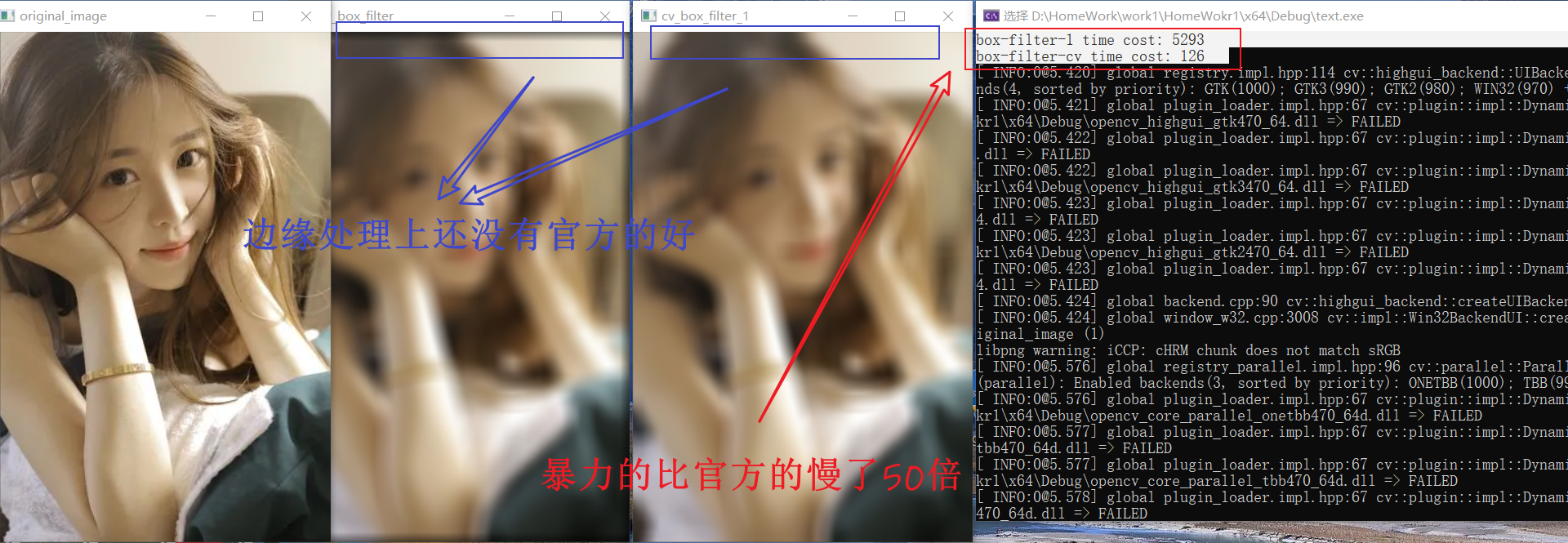
优化过后，在半径为 $9$ 的时候甚至比官网原版的都还要快一些。:+1:
4.2.2常用的过滤器[二维]
:one: : 分离式过滤器
上面已经介绍了一维的过滤器，二维过滤器就是在一维的基础之上构造的。按道理说，任何二维函数都可以使用过滤器。我们可以用一维过滤器构造二维过滤器： 将多个一维的过滤器进行相乘。
$$
f_2(x,y)=f_1(x)f_1(y)b_2[i,j]=b_1[i]b_1[j] \tag{4.2.5}
$$
:two: : 二维三角形过滤器
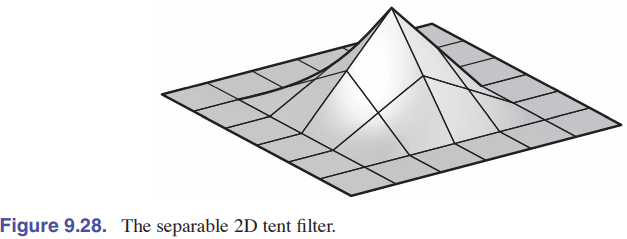$$
f_{2,tent}(x,y)=\begin{cases}
(1-|x|)(1-|y|) &|x|<1 \quad and \quad |y| < 1, \\
0 &otherwise.
\end{cases} \tag{4.2.6}
$$
这个形状沿 $x$ 轴或者 $y$ 轴得到的一维函数都是三角形函数，沿着其他经过原点的直线得到一维函数是二次函数，比如沿着 $x=y$ 得到的函数是 $(1-x^2)$ 。
:three: : 二维高斯过滤器
我们选定方差为 $1$ 的一维高斯滤波器，则二维高斯滤波器的解析式为：
$$
\begin{align*}
f_{2，g}(x,y)&=\frac{1}{2\pi}exp{\frac{x^2+y^2}{-2}}\
&= \frac{1}{2\pi}exp{ \frac{r^2}{-2} }\tag{4.2.7}
\end{align*}
$$
OpenCV提供的高斯滤波函数：
CV_EXPORTS_W void GaussianBlur( InputArray src, OutputArray dst, Size ksize,
double sigmaX, double sigmaY = 0,
int borderType = BORDER_DEFAULT );S
但是我更喜欢自己来实现，高斯滤波器是一种线性滤波器，作用原理和均值滤波类似，都是取滤波窗口内像素均值输出。其窗口模板的系数和均值滤波器不同，均值滤波器的模板系数都是相同的为1；而高斯滤波器的模板系数，则随着距离模板中心的增大而系数减小。所以，高斯滤波器相比于均值滤波器对图像个模糊程度较小。
我们从上面可以得到方差为 $\sigma^2 = 1$ ，均值为 $\mu = 0$ 的时候的二维高斯分布为：
$$
h_{2,gaussian}(x,y) = \frac{1}{2\pi \sigma^2} e^{-\frac{x^2+y^2}{2\sigma^2}} \tag{Gaussian Blur Function}
$$
上面的函数是一个连续函数，并不能够直接应用到图像当中，所以我们要将其离散化。例如要生成一个 $3×3$ Gaussian 模板，我们要以模板的中心位置进行原点取样。
二维高斯模版可以通过矩阵 $M$ 来实现，假设模板大小为 $(2k+1,2k+1)$ ，其中 $k$ 为模版中心，则$M(i,j)$ 如下图所示：
$$
M(i,j) = \frac{1}{2\pi \sigma^2} exp{-\frac{(i-k-1)^2+(j-k-1)^2}{2\sigma^2}} \tag{Gaussian Template}
$$
高斯模版各个位置坐标如下：
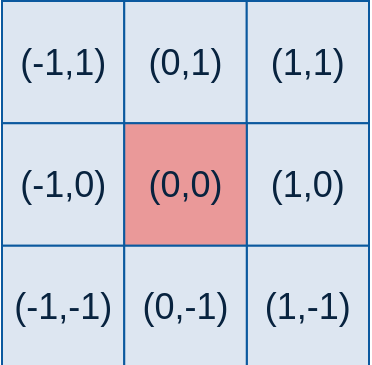
这样计算出来的模板有两种方式： 小数和整数
- 小数形式的模板，直接计算得到的值，没有经过任何处理。
- 整数形式的模板，需要进行归一化处理，将模板左上角的值归一化为1，使用模板的时候需要在前面添加一个系数 $\frac{1}{\sum_{(i,j)\in{\omega} \space \space \omega _{i,j}}}$ 。
Gaussian Template 生成
#include <opencv2\opencv.hpp>
#include <iostream>
#include <string>
#define M_PI 3.1415926
#define KSIZE 3
#define SIGMA 0.8f
#define MAX_TEMPLATE_KSIZE 11
void GenerateGaussianTemplate(double window[][MAX_TEMPLATE_KSIZE], int ksize, double sigma) {
int center = ksize / 2;
double x2, y2;
for (int i = 0; i < ksize; i++) {
x2 = cv::pow(i - center, 2);
for (int j = 0; j < ksize; j++) {
y2 = cv::pow(j - center, 2);
double fxy = cv::exp(-(x2 + y2) / (2 * sigma * sigma));
fxy /= 2 * M_PI * sigma * sigma;
window[i][j]= fxy;
}
}
double k = 1 / window[0][0]; //进行归一化操作
for (int i = 0; i < ksize; i++) {
for (int j = 0; j < ksize; j++) {
window[i][j] *= k;
}
}
}
void PrintGaussianTemplate(double window[][MAX_TEMPLATE_KSIZE], int ksize) {
if (!window || ksize > MAX_TEMPLATE_KSIZE) { std::cout << "Window Template NULL" << std::endl; return; }
for (int row = 0; row < ksize; row++) {
for (int col = 0; col < ksize; col++) {
std::cout << window[row][col] << "\t";
}
std::cout << std::endl;
}
}
int main(void) {
double GaussianTemplateWindow[3][MAX_TEMPLATE_KSIZE] = {0};
GenerateGaussianTemplate(GaussianTemplateWindow, KSIZE, SIGMA);
PrintGaussianTemplate(GaussianTemplateWindow, KSIZE);
}
KSIZE = 3,SIGMA = 0.8 →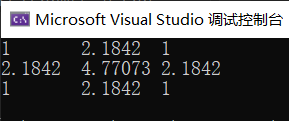
对其取整得到的是整数模板高斯滤波：$\frac1{16}\begin{pmatrix} 1&2&1\2&4&2\1&2&1 \end{pmatrix}$
KSIZE = 5,SIGMA = 1.8 →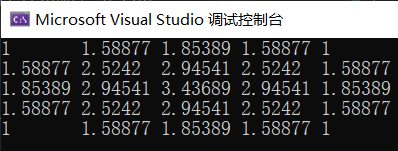 
$\sigma$ 值的意义以及选取意义
实现高斯模板的创建，最重要的就是 $\sigma$ 值的选取。这个值代表着离散程度，如果 $\sigma$ 比较小，那么生成的模板中心系数比较大，周围系数比较小，对图像的平滑效果并不明显。如果 $\sigma$ 比较小，则反之，对图像的效果比较明显。
对于一维的高斯函数：
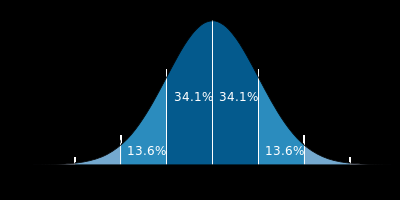
对于二维的高斯函数，我们不能够直接使用 $\sigma$ ，二维的高斯函数可以将 $\sigma$ 分成 $\sigma_x,\sigma_y$ ，为什么？二维高斯从二维正太分布中来，二维正太分布，我们记为 $N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2)$：
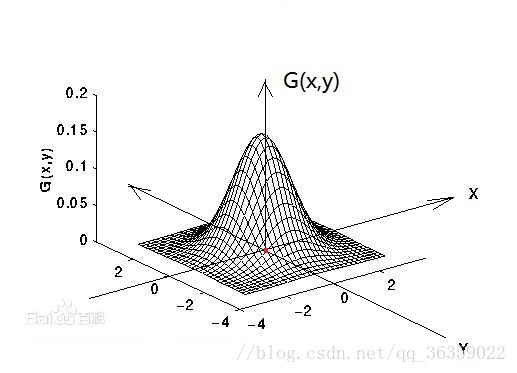
高斯滤波就是将上图的二维正太分布应用在二维矩阵上，$G(x,y)$ 就是矩阵上的权重值，我们将得到的值归一化，将值的范围约束在 $[0,1]$ ，所有的值相加之后得到 $1$。
Gaussian Filter 暴力实现
#include <opencv2/opencv.hpp>
#include <iostream>
#include <ctime>
#include <string>
#define M_PI 3.1415926
#define KSIZE 5
#define SIGMA 15.0f
#define MAX_KSIZE 11
void GenerateGaussianTemplate(double **window, int ksize, double sigma) {
int center = ksize / 2;
double x2, y2,sum;
x2 = 0, y2 = 0, sum = 0;
for (int i = 0; i < ksize; i++) {
x2 = cv::pow(i - center, 2);
for (int j = 0; j < ksize; j++) {
y2 = cv::pow(j - center, 2);
double fxy = cv::exp(-(x2 + y2) / (2 * sigma * sigma));
fxy /= 2 * M_PI * sigma * sigma;
sum += fxy;
window[i][j] = fxy;
}
}
/*double k2 = 0.0f;*/
for (int i = 0; i < ksize; i++) {
for (int j = 0; j < ksize; j++) {
window[i][j] /= sum;
/*k2 += window[i][j];*/
}
}
/*std::cout << k2 << std::endl;*/
}
void PrintGaussianTemplate(double **window, int ksize) {
if (!window || ksize > MAX_KSIZE) { std::cout << "Window Template NULL" << std::endl; return; }
for (int row = 0; row < ksize; row++) {
for (int col = 0; col < ksize; col++) {
std::cout << "[" << window[row][col] << "]\t";
}
std::cout << std::endl;
}
}
void GaussianFilter(const cv::Mat &src,cv::Mat &dst,int ksize,double sigma) {
assert(src.channels() || src.channels() == 3); //仅仅处理单通道图像
if (ksize > MAX_KSIZE) { std::cout << "kszie is too big! Smaller!" << std::endl; return; }
clock_t time_beg = clock();
clock_t time_end = 0;
//申请一个二维数组用于存放生成的高斯模版矩阵
//根据 ksize 生成一个 [ksize,ksize] Matrix
double** templateMatrix = new double* [ksize];
for (int i = 0; i < ksize; i++) { templateMatrix[i] = new double[ksize]; }
GenerateGaussianTemplate(templateMatrix,ksize,sigma);
//将模板应用到图像当中：
int border = ksize / 2; //3->1 5->2
//将src拷贝到dst并且使用 cv::BorderType::BORDER_REFLECT 进行边界的扩充
copyMakeBorder(src, dst, border, border, border, border, cv::BorderTypes::BORDER_REFLECT);
int channels = dst.channels();
int rows = dst.rows - border;
int cols = dst.cols - border;
for (int i = border; i < rows; i++) { //Range : [border,rows-border]
for (int j = border; j < cols; j++) {
double sum[3] = { 0 };
for (int a = -border; a <= border; a++){ //Matrix[2*border,2*border]
for (int b = -border; b <= border; b++){
if (channels == 1)
{ sum[0] += templateMatrix[border + a][border + b] * dst.at<uchar>(i + a, j + b); }
else if (channels == 3) {
cv::Vec3b rgb = dst.at<cv::Vec3b>(i + a, j + b);
auto k = templateMatrix[border + a][border + b];
sum[0] += k * rgb[0];
sum[1] += k * rgb[1];
sum[2] += k * rgb[2];
}
}
}
for (int k = 0; k < channels; k++){
if (sum[k] < 0)
sum[k] = 0;
else if (sum[k] > 255)
sum[k] = 255;
}
if (channels == 1)
dst.at<uchar>(i, j) = static_cast<uchar>(sum[0]);
else if (channels == 3){
cv::Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) };
dst.at<cv::Vec3b>(i, j) = rgb;
}
}
}
// 释放模板数组
for (int i = 0; i < ksize; i++)
delete[] templateMatrix[i];
delete[] templateMatrix;
time_end = clock();
std::cout << "Gaissian blur 1 spend time : " << time_end - time_beg << std::endl;
}
int main(void) {
std::string ImagePath = "C:\\Users\\杨树森\\Desktop\\2.jpg";
cv::Mat ori_image = cv::imread(ImagePath, 1);
cv::Mat dst_image;
GaussianFilter(ori_image, dst_image, KSIZE, SIGMA);
cv::namedWindow("ori_image", 1);
cv::imshow("ori_image", ori_image);
cv::namedWindow("dst_image", 1);
cv::imshow("dst_image", dst_image);
cv::waitKey();
cv::destroyAllWindows();
}
问题①： 为什么要将我们的图像进行边界的扩充，其目的是为了什么？
FROM GPT4 : 因为高斯模板是一个 $ksize \ast{ksize}$ 的矩阵，当我们处理边界像素时，部分模板会超出图像边界。为了解决这个问题，我们需要对图像边界进行扩充，使得边界像素也能够被正确处理。
**问题②：**最起始的两个循环为什么要限定在 $[border,rows - border]$ ?
FROM GPT4 : 问题①已经阐述了为什么需要边界扩充。在这个循环中，我们只处理扩充后的图像的有效区域，即原始图像的区域，所以循环范围是从 border 到 rows-border
问题③： for (int a = -border; a <= border; a++) for (int b = -border; b <= border; b++) 这是什么意思，这个是遍历高斯模板吗？
这两个循环是用来遍历高斯模板的。
由于高斯模板是一个以中心为原点的矩阵，所以我们需要从 -border 到 border 进行遍历。从-board 到 board 并不是遍历了 2*board次，其中还有一个 0 ,所以能够完全遍历高斯模板。这两个循环遍历了高斯模板的所有元素，并将其应用到图像的每个像素上。
问题④： for (int k = 0; k < channels; k++){ if (sum[k] < 0) sum[k] = 0; else if (sum[k] > 255) sum[k] = 255; } 这段代码在总代码中是什么作用，是什么意思？
这段代码的作用是对每个通道的像素值进行范围限制。在图像处理中，像素值的范围通常是0到255。在应用高斯模板后，某些像素值可能会超出这个范围。为了确保结果图像的正确性，我们需要将这些超出范围的像素值进行截断。
这段代码首先遍历图像的通道数（channels），然后检查每个通道的像素值（sum[k]）是否超出了0到255的范围。如果像素值小于0，将其设置为0；如果像素值大于255，将其设置为255。这样可以确保输出图像的像素值在正确的范围内。
Method: cv2.copymakeborder(src,dst,top,buttom,left,right,borderType,value)
src：输入的图像。dst: 输出返回的图像。top,buttom,left,right：分别代表上下左右边界。borderType: 定义边框的类型，可以是一下的类型 ：- ①BORDER_CONSTANT ：添加的边界框像素值为常数（需要额外再给定一个参数）
- ②BORDER_REFLECT ：添加的边框像素将是边界元素的镜面反射，类似于
gfedcba|abcdefgh|hgfedcba - ③BORDER_REFLECT_101 或者 BORDER_DEFAULT ： 和上面类似，但是有一些细微的不同，类似于
gfedcb|abcdefgh|gfedcba - ④BORDER_REPLICATE ： 使用最边界的像素值代替，类似于
aaaaaa|abcdefgh|hhhhhhh - ⑤BORDER_WRAP：貌似是直接去掉靠近的两个像素，然后……&*（）不知道怎么解释。
cdefgh|abcdefgh|abcdefg
- 如果
borderType = cv::BORDER_CONSTANT那么则需要填写最后一个参数value = cv::Scale()
创作等级
会员等级